早教吧作业答案频道 -->数学-->
如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为()A、α=βB、α=2βC、α+β=90°D、α
题目详情
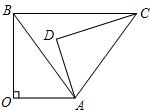 如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )| A、α=β |
| B、α=2β |
| C、α+β=90° |
| D、α+2β=180° |
▼优质解答
答案和解析
考点:
全等三角形的性质
专题:
分析:
根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
∵△AOB≌△ADC,∴AB=AC,∠BAO=∠CAD,∴∠BAC=∠OAD=α,在△ABC中,∠ABC=12(180°-α),∵BC∥OA,∴∠OBC=180°-∠O=180°-90°=90°,∴β+12(180°-α)=90°,整理得,α=2β.故选B.
点评:
本题考查了全等三角形的性质,等腰三角形两底角相等的性质,平行线的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.
考点:
全等三角形的性质
专题:
分析:
根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.
∵△AOB≌△ADC,∴AB=AC,∠BAO=∠CAD,∴∠BAC=∠OAD=α,在△ABC中,∠ABC=12(180°-α),∵BC∥OA,∴∠OBC=180°-∠O=180°-90°=90°,∴β+12(180°-α)=90°,整理得,α=2β.故选B.
点评:
本题考查了全等三角形的性质,等腰三角形两底角相等的性质,平行线的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.
看了 如图,△AOB≌△ADC,点...的网友还看了以下:
判断题关于球体球体是只有面没有棱和顶点的几何体,我是问“球体是只有面没有棱和顶点的几何体吗”,而不是 2020-03-31 …
渐开线齿轮里面的齿顶高系数和顶隙系数是什么?书本上提到说全齿高等于齿顶高加上齿根高;而标准齿顶高h 2020-05-17 …
求二次函数图像y=2—2x2的对称轴和顶点坐标求二次函数图像y=—3(x—1)²+5的对称轴和顶点 2020-06-14 …
某工厂有长4米,宽4米的铁皮,把它围成没有底和顶的正方体形状的产品存放处(底和顶某工厂有长4米,宽 2020-06-15 …
三阶魔方,下面两层、顶面都拼好了,但是顶面四周的角块大部分都不一样,求拼法!三阶魔方!下面两层和顶 2020-06-30 …
如图,两个侧壁绝热、顶部和底部都导热的相同气缸直立放置,气缸底部和顶部均有细管连通,顶部的细管带有 2020-07-10 …
等腰直角三角形ABC的直角顶点C和顶点B都在直线2x+3y-6=0上,求``等腰直角三角形ABC的 2020-07-26 …
齿轮齿顶高系数和顶隙系数对刀具的影响齿轮齿顶高系数和顶隙系数对刀具的影响:假设一:一对渐开线直齿圆 2020-08-01 …
给我魔方顶层同色和顶角归位的公式~就差这两个~谁给以下谢谢了`~我打得是顶面十字—同色—顶棱归位—顶 2020-10-31 …
豌豆花腋生和顶生是一对相对性状,受一对基因B、b控制,下列是几组杂交实验结果.杂交组合亲本表现型后代 2020-11-02 …