早教吧作业答案频道 -->数学-->
如图,平面直角坐标系中,已知点A(1,3),B(2,0),C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.(1)求证:AO=AB;(2)求证:△AOC≌△ABD;
题目详情
如图,平面直角坐标系中,已知点A(1,3),B (2,0),C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
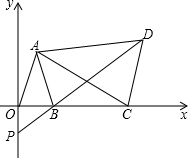
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当∠ACO=30°时,AD=___(直接填写);当点C运动时,点P在y轴上的位置是否发生改变,为什么?

(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当∠ACO=30°时,AD=___(直接填写);当点C运动时,点P在y轴上的位置是否发生改变,为什么?
▼优质解答
答案和解析
(1)如图,作AE⊥OB于点E,
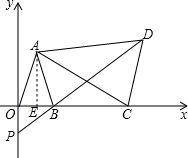
∵A(1,3),B(2,0),
∴OE=1,BE=2-1=1,
∴OE=BE,
在△AEO与△AEB中,
∵
,
∴△AEO≌△AEB,
∴AO=AB;
(2)∵∠CAD=∠OAB,
∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,
在△AOC与△ABD中,
∵
,
∴△AOC≌△ABD(SAS);
(3)当∠ACO=30°时,AD=6;
点P在y轴上的位置不发生改变.
理由:设∠AOB=∠ABO=α,
∵由(2)知,△AOC≌△ABD,
∴∠ABD=∠AOB=α,
∵OB=2,∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,∠POB=90°,
∴OP长度不变.
故答案为:6.

∵A(1,3),B(2,0),
∴OE=1,BE=2-1=1,
∴OE=BE,
在△AEO与△AEB中,
∵
|
∴△AEO≌△AEB,
∴AO=AB;
(2)∵∠CAD=∠OAB,
∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,
在△AOC与△ABD中,
∵
|
∴△AOC≌△ABD(SAS);
(3)当∠ACO=30°时,AD=6;
点P在y轴上的位置不发生改变.
理由:设∠AOB=∠ABO=α,
∵由(2)知,△AOC≌△ABD,
∴∠ABD=∠AOB=α,
∵OB=2,∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,∠POB=90°,
∴OP长度不变.
故答案为:6.
看了 如图,平面直角坐标系中,已知...的网友还看了以下:
若关于的x方程(m-1)x的|m|-1次方-x+2是一元一次方程,求m的值 2020-05-21 …
假设p(x)为F[x]中一个次数>=1的多项式,如果对于F[x]中任意多项式f(x)都有p(x)| 2020-05-23 …
由于乙炔对压力敏感。易发生爆炸,故利用氧乙炔气体进行水下切割时,只能在深度小于()的水中进行。A. 2020-05-31 …
碳溶于( )的γ—Fe中所形成的组织称为奥氏体 A 金属晶体 B 密排立方晶格 2020-05-31 …
你能在下面的X中填上适当的字,使每一行都能成为一个成语吗?(横竖都要的哦)不好意思,忘了~哈哈1. 2020-06-03 …
关于的x一元二次方程X^2-X+P-1=0有两实数根X1,X2.若[2+X1(1-X1)][2+X 2020-06-03 …
关于的x不等式mx2+6mx+m+8大于等于0在R上恒成立,求m的取值范围 2020-06-06 …
关于的x不等式mx2+6mx+m+8大于等于0在R上恒成立,求m的取值范围呃.其实答案我也会求出来 2020-07-15 …
假设p(x)为F[x]中一个次数>=1的多项式,如果对于F[x]中任意多项式f(x)都有p(x)| 2020-07-27 …
关于的x不等式x^logax(x是真数)>x^4.5/a^2的解集是 2020-11-17 …