早教吧作业答案频道 -->数学-->
操作:如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.探究:(1)如图1,当点P在线段BC上时,①若∠BAP=30°,求∠AFE的度数;
题目详情
操作:如图,边长为2的正方形ABCD,点P在射线BC上,将△ABP沿AP向右翻折,得到△AEP,DE所在直线与AP所在直线交于点F.
探究:(1)如图1,当点P在线段BC上时,①若∠BAP=30°,求∠AFE的度数;②若点E恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?并求出此时∠AFD的度数.
归纳:(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;
猜想:(3)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论.
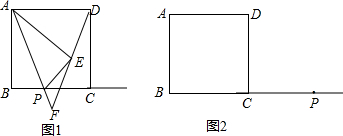
探究:(1)如图1,当点P在线段BC上时,①若∠BAP=30°,求∠AFE的度数;②若点E恰为线段DF的中点时,请通过运算说明点P会在线段BC的什么位置?并求出此时∠AFD的度数.
归纳:(2)若点P是线段BC上任意一点时(不与B,C重合),∠AFD的度数是否会发生变化?试证明你的结论;
猜想:(3)如图2,若点P在BC边的延长线上时,∠AFD的度数是否会发生变化?试在图中画出图形,并直接写出结论.

▼优质解答
答案和解析
(1)①∵∠EAP=∠BAP=30°,
∴∠DAE=90°-30°×2=30°,
在△ADE中,AD=AE,∠DAE=30°,
∴∠ADE=∠AED=(180°-30°)÷2=75°,
在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,
∴∠F=180°-60°-75°=45°;
②点E为DF的中点时,P也为BC的中点,理由如下:
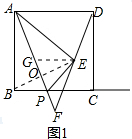
如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,
∵EG∥AD,DE=EF,
∴EG=
AD=1,
∵AB=AE,
∴点A在线段BE的垂直平分线上,
同理可得点P在线段BE的垂直平分线上,
∴AF垂直平分线段BE,
∴OB=OE,
∵GE∥BP,
∴∠OBP=∠OEG,∠OPB=∠OGE,
∴△BOP≌△EOG,
∴BP=EG=1,即P为BC的中点,
∴∠DAF=90°-∠BAF,∠ADF=45°+∠BAF,
∴∠AFD=180°-∠DAF-∠ADF=45°;
(2)∠AFD的度数不会发生变化,
证明:作AG⊥DF于点G,如图1(a)所示,
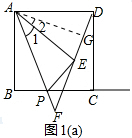
在△ADE中,AD=AE,AG⊥DE,
∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,
∴∠1+∠2=
×90°=45°,即∠FAG=45°,
则∠F=90°-45°=45°;
(3)如图2所示,∠AFE的大小不会发生变化,∠AFE=45°,
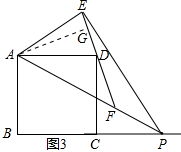
作AG⊥DE于G,得∠DAG=∠EAG,
设∠DAG=∠EAG=α,
∴∠BAE=90°+2α,
∴∠FAE=
∠BAE=45°+α,
∴∠FAG=∠FAE-∠EAG=45°,
在Rt△AFG中,∠AFE=90°-45°=45°.
∴∠DAE=90°-30°×2=30°,
在△ADE中,AD=AE,∠DAE=30°,
∴∠ADE=∠AED=(180°-30°)÷2=75°,
在△AFD中,∠FAD=30°+30°=60°,∠ADF=75°,
∴∠F=180°-60°-75°=45°;
②点E为DF的中点时,P也为BC的中点,理由如下:

如图1,连接BE交AF于点O,作EG∥AD,得EG∥BC,
∵EG∥AD,DE=EF,
∴EG=
| 1 |
| 2 |
∵AB=AE,
∴点A在线段BE的垂直平分线上,
同理可得点P在线段BE的垂直平分线上,
∴AF垂直平分线段BE,
∴OB=OE,
∵GE∥BP,
∴∠OBP=∠OEG,∠OPB=∠OGE,
∴△BOP≌△EOG,
∴BP=EG=1,即P为BC的中点,
∴∠DAF=90°-∠BAF,∠ADF=45°+∠BAF,
∴∠AFD=180°-∠DAF-∠ADF=45°;
(2)∠AFD的度数不会发生变化,
证明:作AG⊥DF于点G,如图1(a)所示,

在△ADE中,AD=AE,AG⊥DE,
∵AG平分∠DAE,即∠2=∠DAG,且∠1=∠BAP,
∴∠1+∠2=
| 1 |
| 2 |
则∠F=90°-45°=45°;
(3)如图2所示,∠AFE的大小不会发生变化,∠AFE=45°,

作AG⊥DE于G,得∠DAG=∠EAG,
设∠DAG=∠EAG=α,
∴∠BAE=90°+2α,
∴∠FAE=
| 1 |
| 2 |
∴∠FAG=∠FAE-∠EAG=45°,
在Rt△AFG中,∠AFE=90°-45°=45°.
看了 操作:如图,边长为2的正方形...的网友还看了以下:
已知二次函数y=ax²+bx+c(a≠0)的图像经过点A(-1,0)与B(5,0),(1)求(b+ 2020-05-16 …
在研究反比例函数y=ax(a≠0)的图象时,我们发现有如下性质:(1)图象是中心对称图形,对称中心 2020-05-16 …
函数f(x)=a^|x-b|(a>0,且a≠1)的图像关于直线X=b对称函数f(x)=a|x-b| 2020-05-22 …
指数函数y=a^x与y=(1/a)^x(a〉0,且a≠1)的图像关于y轴对称,y=(1/a)^x不 2020-06-27 …
二次函数y=ax^2+bx+c(a≠0)的图像如图所示①abc>0②a+b+c=2③a>1/2④b 2020-07-09 …
已知函数y=a+sinbx(b>0且b≠1)的图象如图所示,那么函数y=logb(x-a)的图象可 2020-07-15 …
小丽同学在生日那天收到一个水晶球礼物,透过水晶球可以看到对侧球面上A点的图案,眼睛及A点的位置如图 2020-07-31 …
把二次函数=a(x+h)^2+k(a≠0)的图象先向左平移2个单位,(1)再向上平移4个单位,得到 2020-08-02 …
(2014•淄博)关于x的反比例函数y=a+4x的图象如图,A、P为该图象上的点,且关于原点成中心对 2020-11-13 …
(1)函数f(x+a)与函数f(a-x)的图像关于对称,(2)函数f(x-a)与函数f(a-x)的图 2020-11-18 …