早教吧作业答案频道 -->数学-->
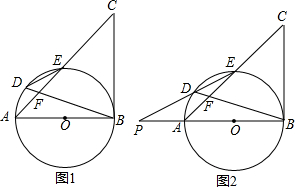
如图I,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交O于点D,且∠BDE=∠CBE.(1)求证:BC是⊙O的切线;(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,求PDDE的值及AO的长
题目详情
如图I,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交O于点D,且∠BDE=∠CBE.
(1)求证:BC是⊙O的切线;
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,求
的值及AO的长.
(1)求证:BC是⊙O的切线;
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,求
| PD |
| DE |

▼优质解答
答案和解析
(1)证明:如图1中,连接BE.
∵AB是直径,
∴∠AEB=90°,
∴∠A+∠ABE=90°,
∵∠A=∠D=∠EBC,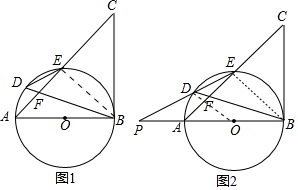
∴∠ABE+∠EBC=90°,
∴∠ABC=90°,
∴AB⊥BC,
∴BC是⊙O的切线.
(2)如图2中,连接OD、BE.
∵BD平分∠ABE,
∴D 是
的中点,
∴OD⊥AE,∵AE⊥BE,
∴BE∥OD,
∵PA=OA=OB,
∴OP=2OB,
∴
=
=
,
∴PD=2DE=6,
∵△PDB∽∠PAF,
∴
=
,
∴PD•PE=PA•PA,
∴3OB2=54,
∴OB=OA=3
.
∵AB是直径,
∴∠AEB=90°,
∴∠A+∠ABE=90°,
∵∠A=∠D=∠EBC,

∴∠ABE+∠EBC=90°,
∴∠ABC=90°,
∴AB⊥BC,
∴BC是⊙O的切线.
(2)如图2中,连接OD、BE.
∵BD平分∠ABE,
∴D 是
 |
| AE |
∴OD⊥AE,∵AE⊥BE,
∴BE∥OD,
∵PA=OA=OB,
∴OP=2OB,
∴
| PD |
| DE |
| OP |
| OB |
| 2 |
| 1 |
∴PD=2DE=6,
∵△PDB∽∠PAF,
∴
| PA |
| PD |
| PE |
| PB |
∴PD•PE=PA•PA,
∴3OB2=54,
∴OB=OA=3
| 2 |
看了 如图I,以△ABC的边AB为...的网友还看了以下:
现规定一种运算:a现规定一种运算a※b=a的平方b,其中a,b为实数,则2a的平方b+(b-a)※ 2020-05-13 …
[(xy+2)(xy-2)-2x的平方y的平方+4]÷(xy)已知A=a的平方-2ab+b的平方B 2020-05-13 …
已知实数a、b满足a的平方=2-2a,b的平方=2-2b,则b/a的平方+a/b的平方为多少它有四 2020-05-15 …
在有理数范围内,下列多项式能用公式法进行因式分解的是A.a的平方-6a B.a的平方-ab+b的平 2020-05-16 …
1、x+2分之2x+x-3分之52、2a+2b分之a-b-a的平方-b的平方分之a的平方+b的平方 2020-06-03 …
有理数的分式题已知a,b,c,d是有理数且x-a的绝对值+(y+b)的平方=0,求试子x+y/a的 2020-07-30 …
提公因式(过程)4(x-2)+2b(2-x)7(a-1)+x(a-1)2(y-x)+3(x-y)4 2020-08-01 …
1(a+b)(a的平方-b的平方)÷(a+b)的平方=2已知A.B都是整式,且A÷x平方=B,若A 2020-08-02 …
如果把分式a+b/a-b中的a,b都变为原来的3/1,那么分式的值会不会改变?如果是分式ab/a-b 2020-12-31 …
已知(a-2)的平方+|b+1|=0求3a的平方b-(a的平方b-3a的平方b)的值.注意,a的平方 2021-01-16 …