早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,直线AB交y轴于A点,交x轴于B点,A(0,6),B(6,0).(1)现在一直角三角板的直角顶点放置于AB的中点C,并绕C点旋转,两直角边分别交x轴、y轴于N、M(如图)两
题目详情
在平面直角坐标系xOy中,直线AB交y轴于A点,交x轴于B点,A(0,6),B(6,0).
(1)现在一直角三角板的直角顶点放置于AB的中点C,并绕C点旋转,两直角边分别交x轴、y轴于N、M(如图)两点,求证:CM=CN;
(2)已知点D(4,6),求点D关于直线AB对称的点的坐标;
(3)若E是线段OB上一点,∠AEO=67.5°,OF⊥AE于G,交AB于F,求
的值.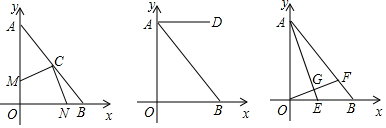
(1)现在一直角三角板的直角顶点放置于AB的中点C,并绕C点旋转,两直角边分别交x轴、y轴于N、M(如图)两点,求证:CM=CN;
(2)已知点D(4,6),求点D关于直线AB对称的点的坐标;
(3)若E是线段OB上一点,∠AEO=67.5°,OF⊥AE于G,交AB于F,求
| GE |
| AE-OF |
▼优质解答
答案和解析
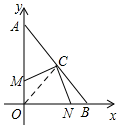 (1)连接OC,
(1)连接OC,
∵OA=OB=6,C为AB的中点,
∴OC⊥AB,OC=AC=BC,
∴∠MOC=45°=∠NBC,
∵∠MCO+∠OCN=∠OCN+∠NCB=90°,
∴∠MCO=∠NCB,
在△OCM和△BCN中,
,
∴△OCM≌△BCN(ASA),
∴CM=CN;
(2)过D作DD′⊥AB于H,交y轴于D′,
∵∠OAB=45°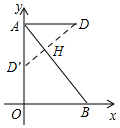 ,
,
∴∠BAD=45°,
∵∠AHD=90°,
∴∠ADD′=45°,
∴AB为DD′的垂直平分线,
∴D′为D点关于AB的对称点,
∵D(4,6),
∴AD′=AD=4,
∴OD′=6-4=2,
∴D′(0,2);
(3)过B作BM⊥OF于M,则∠M=90°,
∵AE⊥OF,∠AOE=90°,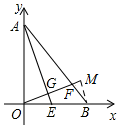
∴∠AGO=∠M=90°,∠OAG=∠BOM,
在△AOG和△OBM中,
,
∴△AOG≌△OBM(AAS),
∴AG=OM,OG=BM,
∵∠AEO=67.5°,OF⊥AE,∠AOE=90°,
∴∠EOG=22.5°=∠OAG,
又∵∠OAB=45°,
∴∠BAE=22.5°,
∵AE∥BM,
∴∠MBF=∠BAE=22.5°,
∴∠FBM=∠EOG,
在△OGE和△BFM中,
,
∴△OGE≌△BFM(ASA),
∴GE=FM,
∵AE=AG+GE,OF=OM-FM,
∴AE-OF=(AG+GE)-(OM-FM)=GE+FM=2GE,
∴
=
=
.
 (1)连接OC,
(1)连接OC,∵OA=OB=6,C为AB的中点,
∴OC⊥AB,OC=AC=BC,
∴∠MOC=45°=∠NBC,
∵∠MCO+∠OCN=∠OCN+∠NCB=90°,
∴∠MCO=∠NCB,
在△OCM和△BCN中,
|
∴△OCM≌△BCN(ASA),
∴CM=CN;
(2)过D作DD′⊥AB于H,交y轴于D′,
∵∠OAB=45°
 ,
,∴∠BAD=45°,
∵∠AHD=90°,
∴∠ADD′=45°,
∴AB为DD′的垂直平分线,
∴D′为D点关于AB的对称点,
∵D(4,6),
∴AD′=AD=4,
∴OD′=6-4=2,
∴D′(0,2);
(3)过B作BM⊥OF于M,则∠M=90°,
∵AE⊥OF,∠AOE=90°,

∴∠AGO=∠M=90°,∠OAG=∠BOM,
在△AOG和△OBM中,
|
∴△AOG≌△OBM(AAS),
∴AG=OM,OG=BM,
∵∠AEO=67.5°,OF⊥AE,∠AOE=90°,
∴∠EOG=22.5°=∠OAG,
又∵∠OAB=45°,
∴∠BAE=22.5°,
∵AE∥BM,
∴∠MBF=∠BAE=22.5°,
∴∠FBM=∠EOG,
在△OGE和△BFM中,
|
∴△OGE≌△BFM(ASA),
∴GE=FM,
∵AE=AG+GE,OF=OM-FM,
∴AE-OF=(AG+GE)-(OM-FM)=GE+FM=2GE,
∴
| GE |
| AE-OF |
| GE |
| 2GE |
| 1 |
| 2 |
看了 在平面直角坐标系xOy中,直...的网友还看了以下:
求顶点坐标有一个单位圆,设单位圆与x轴交于PQ两点,另有一点M在原上(异于PQ),然后PM交x=3 2020-05-13 …
如图直线y=-x+3交x轴于B,交y于C,顶点为E的抛物线y=-x2+bx+c经过BC两点,与x轴 2020-05-16 …
已知二次函数y=x^2-(m^2+8)x+2(m^2+6),设抛物线顶点为A,与X轴交于B,C两点 2020-05-16 …
初三数学一个二次函数的图像是以(4,-2)为顶点的抛物线,其与x轴交于A、B两点,与y轴交于C点, 2020-05-16 …
如图,二次函数y=1/2x-x+c的图象与x轴分别交于A、B两点,顶点M关于x轴的对称点是M’20 2020-06-03 …
抛物线y=x^2-2x-3与x轴交与A,B两点,与y轴交与C点.设直线y=-x+3与y轴的交点抛物 2020-06-14 …
已知直线y=-x+2与x轴交于A点,与y轴交于B点,一抛物线经过A,B两点且对称轴为x=2求:1, 2020-07-22 …
已知二次函数y=x的平方-2x-3与x轴交于AB两点(A在B左边),交y轴于C,顶点为P,在抛物已知 2020-11-27 …
已知二次函数y=x的平方-4x+3图像与x轴交与A,B两点(点A在点B的左边),与y轴交与点c,顶点 2021-01-10 …
如图,一个二次函数的图像与x轴交于A,B两点(A在B的左边),与y轴交于点c,起顶点坐标(-1,-8 2021-01-10 …