早教吧作业答案频道 -->数学-->
如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.(1)判断直线DE与半圆O的位置关系,并说明理由
题目详情
如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
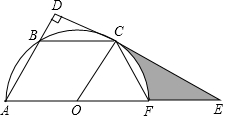
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.

(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.
▼优质解答
答案和解析
(1)结论:DE是⊙O的切线.
理由:∵四边形OABC是平行四边形,
又∵OA=OC,
∴四边形OABC是菱形,
∴OA=OB=AB=OC=BC,
∴△ABO,△BCO都是等边三角形,
∴∠AOB=∠BOC=∠COF=60°,
∵OB=OF,
∴OG⊥BF,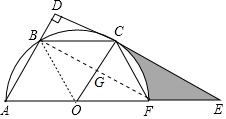
∵AF是直径,CD⊥AD,
∴∠ABF=∠DBG=∠D=∠BGC=90°,
∴四边形BDCG是矩形,
∴∠OCD=90°,
∴DE是⊙O的切线.
(2)①由(1)可知:∠COF=60°,OC=OF,
∴△OCF是等边三角形,
∴CF=OC.
②在Rt△OCE中,∵OC=12,∠COE=60°,∠OCE=90°,
∴OE=2OC=24,EC=12
,
∵OF=12,
∴EF=12,
∴
的长=
=4π,
∴阴影部分的周长为4π+12+12
.
理由:∵四边形OABC是平行四边形,
又∵OA=OC,
∴四边形OABC是菱形,
∴OA=OB=AB=OC=BC,
∴△ABO,△BCO都是等边三角形,
∴∠AOB=∠BOC=∠COF=60°,
∵OB=OF,
∴OG⊥BF,

∵AF是直径,CD⊥AD,
∴∠ABF=∠DBG=∠D=∠BGC=90°,
∴四边形BDCG是矩形,
∴∠OCD=90°,
∴DE是⊙O的切线.
(2)①由(1)可知:∠COF=60°,OC=OF,
∴△OCF是等边三角形,
∴CF=OC.
②在Rt△OCE中,∵OC=12,∠COE=60°,∠OCE=90°,
∴OE=2OC=24,EC=12
| 3 |
∵OF=12,
∴EF=12,
∴
 |
| CF |
| 60π•12 |
| 180 |
∴阴影部分的周长为4π+12+12
| 3 |
看了 如图,已知平行四边形OABC...的网友还看了以下:
(2009•大连)如图1,在△ABC和△PQD中,AC=kBC,DP=kDQ,∠C=∠PDQ,D、 2020-05-24 …
化学(关于鉴别)如何鉴别CO,H2,CH4,三种无色气体,简要写出操作步骤及有关的化学方程式(3个 2020-06-14 …
谁能善于把别人的长处集于一身,谁就会是胜利者,还能用别的例子证明这这句话说的道理吗谁能善于把别人的 2020-06-18 …
数学问题有关1+1听说有个科学家用几十年去证明1+1=2,我想知道他是怎么证明的?还有1+1是不是 2020-07-21 …
如图,已知∠AOB.小明按如下步骤作图:(1)以点O为圆心,适当长为半径画弧,交OA于D,交OB于 2020-07-29 …
如图,已知AC垂直于BC,垂足为C,且AC和BC分别为BAD和ABE的平分线,说明AD如图,已知AC 2020-11-03 …
(2013•昆明)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相 2020-11-08 …
大家帮忙找找关于退一步海阔天空,关于阳光总在风雨后的名人名言(要有名人名字,不要有错别字).撑乱懒? 2020-12-14 …
如图,△ABC内接于圆O,∠BAC的平分线分别交圆O,BC于点D如图,△ABC内接于圆O,∠BAC的 2021-01-09 …
(2014•昆明)如图中甲为中国疆域示意图,乙为我国东海防空识别区图.据图回答下列问题.(1)东海防 2021-01-22 …