早教吧作业答案频道 -->数学-->
四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,若该四棱锥的所有顶点都在体积为243π16同一球面上,则PA=.
题目详情
四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AB=2,若该四棱锥的所有顶点都在体积为
同一球面上,则PA=___.
| 243π |
| 16 |
▼优质解答
答案和解析
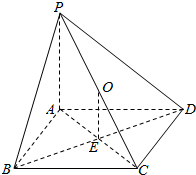 连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为
连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为
PC=
=
,
所以由球的体积可得
π(
)3=
,解得PA=
,
故答案为:
.
 连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为
连结AC,BD交于点E,取PC的中点O,连结OE,则OE∥PA,所以OE⊥底面ABCD,则O到四棱锥的所有顶点的距离相等,即O球心,均为| 1 |
| 2 |
| 1 |
| 2 |
| PA2+AC2 |
| 1 |
| 2 |
| PA2+8 |
所以由球的体积可得
| 4 |
| 3 |
| 1 |
| 2 |
| PA2+8 |
| 243π |
| 16 |
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
看了 四棱锥P-ABCD的底面AB...的网友还看了以下:
已知a是3个正数a.b.c中最大的数,且a/b=c/d,则a+d于c+d的大小关系是?(则a+d于c 2020-03-31 …
关于质点做匀速圆周运动的说法正确的是()A.由a=v2r可知,a与r成反比B.由a=v2r可知,a 2020-05-13 …
找错并改正(英语题)( ) 1.It"s [a] beautiful and [sun] day. 2020-05-13 …
在0.1mol.L-1的Na2S溶液中,含有多种分子和离子,下列关系不正确的是(D) A.c(S2 2020-05-16 …
关于人体衰老细胞和癌细胞的叙述,正确的是()A.癌细胞与衰老细胞都有基因表达B.癌变和衰老都是细胞 2020-07-25 …
A在塔底D的正西面,在A处测得塔顶C的仰角为45°,B在塔底D的南偏东60°处,在塔顶C处测得到B的 2020-11-11 …
aW、bX、cC、dZ、eR是五种短周期元素,e-d=d-c=c-b=b-a=4,其中一种是常见金属 2020-11-26 …
明天就考了,已有如下定义和输入语句:inta1,a2;charc1,c2;scanf("%d%d%c 2020-12-24 …
四个带等量电荷的小球a、b、c、d,已知d带正电.它们之间相互作用的情况如图所示,则下列判断中正确的 2020-12-24 …
,AB为弧形光滑轨道,CD是一半为R的竖直放置的半圆形光滑轨道,D点在C点AB为弧形光滑轨道,CD是 2020-12-25 …