如图，在平面直角坐标系xOy中，已知椭圆C：x2a2+y2b2=1（a>b>0）的离心率为223，经过椭圆的左顶点A（-3，0）作斜率为k（k≠0）的直线l交椭圆C于点D，交轴于点E（1）求椭圆C的方程；（2）

Question

如图，在平面直角坐标系xOy中，已知椭圆C：(x2)/(a2)+(y2)/(b2)=1（a>b>0）的离心率为(2√(2))/(3)，经过椭圆的左顶点A（-3，0）作斜率为k（k≠0）的直线l交椭圆C于点D，交轴于点E

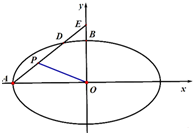
（1）求椭圆C的方程；
（2）已知点P为线段AD的中点，是否存在定点Q，对于任意的k（k≠0）都有OP⊥EQ，若存在，求出点Q的坐标，若不存在，说明理由．

Answer 1

（1）由题意，a=3，(c)/(a)=(2√(2))/(3)，
∴c=2√(2)，b=1，
∴椭圆C的方程(x2)/(9)+y²=1；
（2）设直线的方程为y=k（x+3），
代入椭圆方程，消元得（9k²+1）x²+54k²x+81k²-9=0，
∴x=-3或(3-27k2)/(9k2+1)…（6分）
∴D（(3-27k2)/(9k2+1)，(6k)/(9k2+1)），
又∵点P为AD的中点，∴P（-(27k2)/(9k2+1)，(3k)/(9k2+1)），
则k_OP=-(1)/(9k)（k≠0），…（9分）
直线l的方程为y=k（x+3），令x=0，得E（0，3k），
假设存在定点Q（m，n）（m≠0）使得OP⊥EQ，则k_OP•k_EQ=-1，
即-(1)/(9k)•(n-3k)/(m)=-1，
∴（9m-3）k+n=0恒成立
∴

9m-3=0

n=0

，即m=(1)/(3)，n=0，
因此定点Q的坐标为（(1)/(3)，0）…（12分）