早教吧作业答案频道 -->数学-->
如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H.(1)求证:AH=BH;(2)若∠BAC=60°,求FGDG的值.
题目详情
如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H.
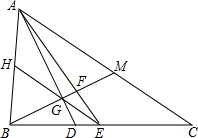
(1)求证:AH=BH;
(2)若∠BAC=60°,求
的值.

(1)求证:AH=BH;
(2)若∠BAC=60°,求
| FG |
| DG |
▼优质解答
答案和解析
(1)证明:∵BF⊥AD,
∴∠ABG+∠BAG=90°,∠AMG+∠MAG=90°,
∵AD是角平分线,
∴∠BAG=∠MAG,
∴∠ABG=∠AMG,
∴AB=AM,
∴BG=MG,
∵BE=EC,
∴GE∥AC,
∴
=
,
∴AH=BH;
(2)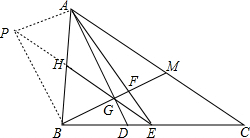 延长EH到P,使GH=HP,连接AP和BP,
延长EH到P,使GH=HP,连接AP和BP,
∵AH=BH,
∴四边形APBG是平行四边形,
∴AP=BG,AP∥BG,
∴
=
,
∴
=
,
同理,
=
,
∴
=
,
∴
=
,
∵∠BAC=60°,AD是角平分线,
∴∠BAG=30°,
在Rt△ABG中,
=tan30°=
,
∴
=
.
∴∠ABG+∠BAG=90°,∠AMG+∠MAG=90°,
∵AD是角平分线,
∴∠BAG=∠MAG,
∴∠ABG=∠AMG,
∴AB=AM,
∴BG=MG,
∵BE=EC,
∴GE∥AC,
∴
| BH |
| AH |
| BE |
| CE |
∴AH=BH;
(2)
 延长EH到P,使GH=HP,连接AP和BP,
延长EH到P,使GH=HP,连接AP和BP,∵AH=BH,
∴四边形APBG是平行四边形,
∴AP=BG,AP∥BG,
∴
| GF |
| PA |
| GE |
| PE |
∴
| GF |
| BG |
| GE |
| PE |
同理,
| GD |
| AG |
| GE |
| PE |
∴
| GF |
| BG |
| GD |
| AG |
∴
| GF |
| GD |
| BG |
| AG |
∵∠BAC=60°,AD是角平分线,
∴∠BAG=30°,
在Rt△ABG中,
| BG |
| AG |
| ||
| 3 |
∴
| FG |
| DG |
| ||
| 3 |
看了 如图,在△ABC中,AC>A...的网友还看了以下:
已知a满足 根号(2006-a)^2 +根号(a-2007)=a 求a-2006^2的值1)已知a 2020-04-05 …
0.5molH2O含个H2O共含有个原子,它的质量是g求详解 2020-04-25 …
已知函数f(x)=x|x-a|的定义域为D,其中a为常数;(1)若D=R,且f(x)是奇函数,求a 2020-05-13 …
已知BE,CE分别是三角形ABC的中线,且交点是G求证;GB;GE=GC;GF=2 2020-05-16 …
ANSYS软件3d实体单元有限元建模分析作业,图示实心扭杆弹簧由半径为R1的内轴和外半径为R0的套 2020-05-17 …
语文拼音中的声介合母与随韵母子怎么拼读?如gu-a=gua前面的gu是不是相拼后才与后面的a相拼? 2020-06-17 …
1.设集合A={a,b,c,d,e},集合B={c,d,f,g},求A交B,A并B.2.设全集U= 2020-07-30 …
1.设集合U=R,Q是有理数集,求补集Q.2.设集合A={s,b,c,d,e},集合B={c,d, 2020-07-30 …
已知(2x-1)的6次方=ax6次+bx5次+cx4次+dx3次+ex2+fx+g求a+b+c+d+ 2020-12-17 …
某生物基因单链的一段是┅G-C-A-G-A-C-A-A-A┅若以此链为模板,经转录翻译形成的多肽链上 2020-12-18 …