早教吧作业答案频道 -->数学-->
如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.(1)写出图中所有的等腰三角形;(2)若∠AED=114°,求∠ABD和∠ACB的度数.
题目详情
如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.
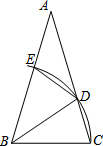
(1)写出图中所有的等腰三角形;
(2)若∠AED=114°,求∠ABD和∠ACB的度数.

(1)写出图中所有的等腰三角形;
(2)若∠AED=114°,求∠ABD和∠ACB的度数.
▼优质解答
答案和解析
(1)∵∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
∵BE=BD=BC,
∴△BCD,△BED是等腰三角形;
∴图中所有的等腰三角形有:△ABC,△BCD,△BED;
(2) ∵∠AED=114°,
∴∠BED=180°-∠AED=66°.
∵BD=BE,
∴∠BDE=∠BED=66°.
∴∠ABD=180°-66°×2=48°.
解法一:设∠ACB=x°,
∴∠ABC=∠ACB=x°.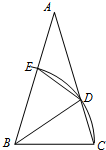
∴∠A=180°-2x°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠BDC为△ABD的外角,
∴∠BDC=∠A+∠ABD.
∴x=180-2x+48,解得:x=76.
∴∠ACB=76°.(10分)
解法二:设∠ACB=x°,
∴∠ABC=∠ACB=x°.
∴∠DBC=x°-48°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠DBC+∠BCD+∠BDC=180°,
∴x-48+x+x=180,解得:x=76.
∴∠ACB=76°.
∴AB=AC,
∴△ABC是等腰三角形;
∵BE=BD=BC,
∴△BCD,△BED是等腰三角形;
∴图中所有的等腰三角形有:△ABC,△BCD,△BED;
(2) ∵∠AED=114°,
∴∠BED=180°-∠AED=66°.
∵BD=BE,
∴∠BDE=∠BED=66°.
∴∠ABD=180°-66°×2=48°.
解法一:设∠ACB=x°,
∴∠ABC=∠ACB=x°.

∴∠A=180°-2x°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠BDC为△ABD的外角,
∴∠BDC=∠A+∠ABD.
∴x=180-2x+48,解得:x=76.
∴∠ACB=76°.(10分)
解法二:设∠ACB=x°,
∴∠ABC=∠ACB=x°.
∴∠DBC=x°-48°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠DBC+∠BCD+∠BDC=180°,
∴x-48+x+x=180,解得:x=76.
∴∠ACB=76°.
看了 如图,已知△ABC中,∠AB...的网友还看了以下:
关于圆周率的描述中,错误的是().A,圆周率是一个常数B,圆周率是一个无限不关于圆周率的描述中,错 2020-05-14 …
已知在椭圆E:x的平方/a的平方+y的平方/b的平方=1(a>b>0)中,以F1(-C,0)为圆心 2020-05-22 …
若圆A中圆心角为60度的弧长与圆B中圆心角为45度的弧长相等,则圆A与圆B的面积比为 2020-05-23 …
在下面的圆柱和圆锥中,A、B、C的底面积相等,A、B、D的高相等,D的底面积是A的3倍,C的高是其 2020-06-03 …
已知圆A:(x+5)平方+y平方=49圆B:(x-5)平方+y平方=1(1)设P(-1,4)为圆A 2020-06-29 …
圆B与圆C的面积之和等于圆A面积的5分之4,且圆A中的阴影部分占圆A面积的6分之1,圆B中的阴影部 2020-07-21 …
一圆台可绕通过圆台中心O且垂直于台面的竖直轴转动.在圆台上放置一小木块A,它随圆台一起做匀速圆周运 2020-07-25 …
圆B与圆C的面积之和等于圆A面积的5分之4,且圆A中的阴影部分占圆A面积的6分之1,圆B中的阴影部 2020-07-31 …
如图所示,水平放置的绝缘桌面上有一个金属环,竖直的条形磁铁从圆环左上方沿水平方向快速移动到右上方,在 2020-11-01 …
如图所示,在一水平、固定的闭合导体圆环上方.有一条形磁铁(N极朝上,S极朝下)由静止开始下落,磁铁从 2021-01-13 …