早教吧作业答案频道 -->数学-->
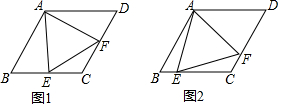
如图,在菱形ABCD中,∠BAD=120°,点E是边BC上的动点(不与点B,C重合),以AE为边作∠EAF,使得∠EAF=12∠BAD,射线AF交边CD于点F.(1)如图1,当点E是边CB的中点时,判断并证明线段AE,AF之间
题目详情
如图,在菱形ABCD中,∠BAD=120°,点E是边BC上的动点(不与点B,C重合),以AE为边作∠EAF,使得∠EAF=
∠BAD,射线AF交边CD于点F.
(1)如图1,当点E是边CB的中点时,判断并证明线段AE,AF之间的数量关系;
(2)如图2,当点E不是边BC的中点时,求证:BE=CF.
| 1 |
| 2 |
(1)如图1,当点E是边CB的中点时,判断并证明线段AE,AF之间的数量关系;
(2)如图2,当点E不是边BC的中点时,求证:BE=CF.

▼优质解答
答案和解析
(1)AE=AF,理由如下:
连接AC.如图所示: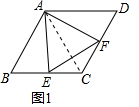
∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,
∴∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS).
∴AE=AF.
(2)证明:由(1)得:∠B=60°,△ABCA是等边三角形,∠EAF=60°,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠BAC=∠EAF=60°,
∴∠BAC-∠EAC=∠EAF-∠EAC,
∴∠BAE=∠CAF,
∵四边形ABCD是菱形,∠BAD=120°,
∴∠BCD=∠BAD=120°,
∴∠ACD=∠BCD-∠BAC=60°,
∴∠ACD=∠B=60°,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴BE=CF.
连接AC.如图所示:

∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,
∴∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
|
∴△ABE≌△ACF(AAS).
∴AE=AF.
(2)证明:由(1)得:∠B=60°,△ABCA是等边三角形,∠EAF=60°,
∴AB=AC,∠BAC=∠ACB=60°,
∴∠BAC=∠EAF=60°,
∴∠BAC-∠EAC=∠EAF-∠EAC,
∴∠BAE=∠CAF,
∵四边形ABCD是菱形,∠BAD=120°,
∴∠BCD=∠BAD=120°,
∴∠ACD=∠BCD-∠BAC=60°,
∴∠ACD=∠B=60°,
在△ABE和△ACF中,
|
∴△ABE≌△ACF(ASA).
∴BE=CF.
看了 如图,在菱形ABCD中,∠B...的网友还看了以下:
10、设函数f(x)=2x-cosx,{an}是公差为π/8的等差数列,f(a1)+f(a2)+… 2020-04-05 …
设函数f(x)=xa+ebx在(-∞,+∞)内连续,且limx→−∞f(x)=0,则常数a,b满足 2020-06-12 …
如图电路,a、b、c分别表示电流表或电压表,电表都是理想的,则下列各组电表示数中可能的是()A.a 2020-06-16 …
如果要使a+b>0且ab<0,那么只要()A.a>0且b<0B.a<0且b>0C.a和b异号D.a 2020-07-30 …
已知命题“∀a,b∈R,如果ab>0,则a>0”,则它的否命题是()A.∀a,b∈R,如果ab<0 2020-08-01 …
“a2+b2≠0”的含义为()A.a和b都不为0B.a和b至少有一个为0C.a和b至少有一个不为0D 2020-10-31 …
若a+b<0,ab<0,则()A.a>0,b>0B.a<0,b<0C.a,b两数一正一负,且正数的绝 2021-01-22 …
如果a+b>0,且ab<0,那么()A.a>0,b>0B.a<0,b<0C.a、b异号且正数的绝对值 2021-01-22 …
已知两个有理数a,b,如果ab<0,且a+b<0,那么()A.a>0,b>0B.a<0,b>0C.a 2021-01-22 …
如果a+b>0,a•b<0,那么()A.a>0,b>0B.a、b异号且负数的绝对值较大C.a<0,b 2021-01-22 …