早教吧作业答案频道 -->数学-->
课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.(1)加工成的正方形零件的边长是多
题目详情
课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
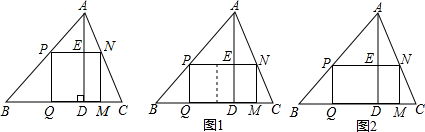
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.

▼优质解答
答案和解析
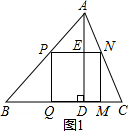 (1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴
=
,即
=
,
解得x=48.
∴加工成的正方形零件的边长是48mm;
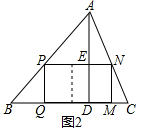
(2)如图2,设PQ=x,则PN=2x,AE=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴
=
,即
=
,
解得:x=
,
∴2x=
,
∴这个矩形零件的两条边长分别为
mm,
mm;
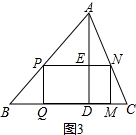
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴
=
,
即
=
,
解得:PQ=80-
x.
则S=PN•PQ=x(80-
x)=-
x2+80x=-
(x-60)2+2400,
故S的最大值为2400mm2,此时PN=60mm,PQ=80-
×60=40(mm).
 (1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,∴AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴
| PN |
| BC |
| AE |
| AD |
| x |
| 120 |
| 80-x |
| 80 |
解得x=48.
∴加工成的正方形零件的边长是48mm;

(2)如图2,设PQ=x,则PN=2x,AE=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴
| PN |
| BC |
| AE |
| AD |
| 2x |
| 120 |
| 80-x |
| 80 |
解得:x=
| 240 |
| 7 |
∴2x=
| 480 |
| 7 |

∴这个矩形零件的两条边长分别为
| 240 |
| 7 |
| 480 |
| 7 |
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴
| PN |
| BC |
| AE |
| AD |
即
| x |
| 120 |
| 80-PQ |
| 80 |
解得:PQ=80-
| 2 |
| 3 |
则S=PN•PQ=x(80-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故S的最大值为2400mm2,此时PN=60mm,PQ=80-
| 2 |
| 3 |
看了 课本中有一道作业题:有一块三...的网友还看了以下:
平面直角坐标系中四边形的存在性问题在平面直角坐标中,有点O(0,0),A(-1,1),B(2,2)( 2020-03-31 …
如图所示,A、B、C是边长为l的等边三角形的三个顶点,D为三角形的中心,①若在A、B、C三顶点处分 2020-04-11 …
如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4 2020-04-27 …
在三角形角ABC中A,B,C所对应的边分别为a,b,c两顶点坐标A(-2,0)B(2,0),且ab 2020-05-16 …
( )是世界上国家间面积最大的陆地争议地区.A.中俄边界争议面积B.中越边界争议面积C.中印边界争 2020-05-17 …
一质点沿两个半径为R的圆弧从A运动到C,所用时间为t,求这个过程中物体的平均速率和平均速度图是中间 2020-05-23 …
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数 2020-07-19 …
(2007•南昌)实验与探究:(1)在图1,2,3中,已知平行四边形ABCD的三个顶点A,B,D的 2020-07-22 …
已知三角形三个顶点的坐标.已知三角形三个顶点的坐标分别为A(4,1),B(0,3),C(2,4), 2020-08-01 …
下列说法中正确的是()A△ABC中BC边上的高线是过顶点A向对边所引的垂线.B△ABC中BC边上的高 2021-02-03 …