如图所示，Rt△ABO中，∠AOB=90°，点A在第一象限，点B在第四象限，且AO：BO=1：2，若点A（x0，y0）的坐标（x0，y0）满足y0=1y0，则点B（x，y）的坐标x，y所满足的关系式为（）A.y=-2xB.y=-2xC.

Question

如图所示，Rt△ABO中，∠AOB=90°，点A在第一象限，点B在第四象限，且AO：BO=1：

√(2)，若点A（x₀，y₀）的坐标（x₀，y₀）满足y₀=(1)/(y0)，则点B（x，y）的坐标x，y所满足的关系式为（　　）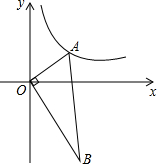

A. y=

(-2)/(x)

B. y=

(-√(2))/(x)

C. y=

(-1)/(x)

D. y=

(1)/(x)

Answer 1

设点B坐标为（x，y），分别过点A、B作AC，BD分别垂直y轴于点C、D，
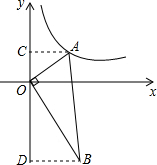
∵∠ACO=∠BDO=90°，
∠AOC+∠BOD=90°，
∠AOC+∠OAC=90°，
∴∠OAC=∠BOD，
∴△AOC∽△OBD，
∴(S△AOC)/(S△BOD)=((OA)/(0B))2=((1)/(√(2)))2=(1)/(2)，
∵点A（x₀，y₀）的坐标x₀，y₀满足y₀=(1)/(y0)，
∴S_△AOC=(1)/(2)，
∴S_△BOD=1，
而点B坐标为（x，y），
∴(1)/(2)x•（-y）=1，
∴y=-(2)/(x)．
故选A