早教吧作业答案频道 -->数学-->
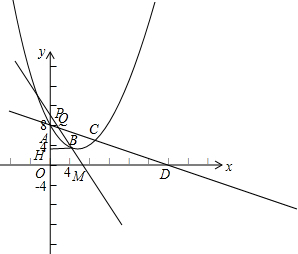
已知,如图,在平面直角坐标系xOy中,二次函数y=ax2-73x+c的图象经过点、A(0,8)、B(6,2)、C(9,m),延长AC交x轴于点D.(1)求这个二次函数的解析式及的m值;(2)求∠ADO的余切值;
题目详情
已知,如图,在平面直角坐标系xOy中,二次函数y=ax2-
x+c的图象经过点、A(0,8)、B(6,2)、C(9,m),延长AC交x轴于点D.
(1)求这个二次函数的解析式及的m值;
(2)求∠ADO的余切值;
(3)过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P(点A的上方)、M、Q,使以点P、A、Q为顶点的三角形与△MDQ相似,求此时点P的坐标.
| 7 |
| 3 |
(1)求这个二次函数的解析式及的m值;
(2)求∠ADO的余切值;
(3)过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P(点A的上方)、M、Q,使以点P、A、Q为顶点的三角形与△MDQ相似,求此时点P的坐标.
▼优质解答
答案和解析
 (1)把A(0,8)、B(6,2)代入y=ax2-
(1)把A(0,8)、B(6,2)代入y=ax2-
x+c,得
,
解得
,
故该二次函数解析式为:y=
x2-
x+8.
把C(9,m),代入y=
x2-
x+8得到:m=y=
×92-
×9+8=5,即m=5.
综上所述,该二次函数解析式为y=
x2-
x+8,m的值是5;
(2)由(1)知,点C的坐标为:(9,5),
又由点A的坐标为(0,8),
所以直线AC的解析式为:y=-
x+8,
令y=0,则0=-
x+8,
解得x=24,
即OD=24,
所以cot∠ADO=
=
=3,即cot∠ADO=3;
(3)在△APQ与△MDQ中,∠AQP=∠MQD.
要使△APQ与△MDQ相似,则∠APQ=∠MDQ或∠APQ=∠DMQ(根据题意,这种情况不可能),
∴cot∠APQ=cot∠MDQ=3.
作BH⊥y轴于点H,
在直角△PBH中,cot∠P=
=3,
∴PH=18,OP=20,
∴点P的坐标是(0,20).
 (1)把A(0,8)、B(6,2)代入y=ax2-
(1)把A(0,8)、B(6,2)代入y=ax2-| 7 |
| 3 |
|
解得
|
故该二次函数解析式为:y=
| 2 |
| 9 |
| 7 |
| 3 |
把C(9,m),代入y=
| 2 |
| 9 |
| 7 |
| 3 |
| 2 |
| 9 |
| 7 |
| 3 |
综上所述,该二次函数解析式为y=
| 2 |
| 9 |
| 7 |
| 3 |
(2)由(1)知,点C的坐标为:(9,5),
又由点A的坐标为(0,8),
所以直线AC的解析式为:y=-
| 1 |
| 3 |
令y=0,则0=-
| 1 |
| 3 |
解得x=24,
即OD=24,
所以cot∠ADO=
| OD |
| OA |
| 24 |
| 8 |
(3)在△APQ与△MDQ中,∠AQP=∠MQD.
要使△APQ与△MDQ相似,则∠APQ=∠MDQ或∠APQ=∠DMQ(根据题意,这种情况不可能),
∴cot∠APQ=cot∠MDQ=3.
作BH⊥y轴于点H,
在直角△PBH中,cot∠P=
| PH |
| BH |
∴PH=18,OP=20,
∴点P的坐标是(0,20).
看了 已知,如图,在平面直角坐标系...的网友还看了以下:
根据下列条件,写出二次函数的解析式1.当x=2时,函数的最大值是1,且图像与x轴的两个交点之间的距离 2020-03-30 …
求二次函数关系式,急用!(1)已知某二次函数的最大值为2,图像的顶点在直线y=x+1上,并且图像经 2020-04-27 …
关于二次函数的问题某二次函数的最大值为2,图像的顶点在y=x+1上,且图像经过点(3,-1),此二 2020-05-13 …
已知二次函数y=ax的平方+bx+c的最大值为2,图像顶点在y=x+1上,并且图像过点(3,-6) 2020-05-16 …
已知二次函数y=ax平方+bx+c的最大值是2,图像的顶点在直线y=x+1上,并且函数图像经过点( 2020-05-16 …
函数f(x)=ax2+bx-2/3的图象关于直线x=-3/2对称(1219:50:48)1、已知函 2020-06-05 …
二次函数y=ax2+2图像通过边长为1且边与坐标轴平行的正方形的两个顶点,那么a=? 2020-07-25 …
已知,如图,直线AB经过点B(0,6),且tan∠ABO=23,与抛物线y=ax2+2在第一象限内 2020-07-26 …
初三数学二次函数!大晚上很急谢谢抛物线y=ax2的对称轴是,顶点坐标是,a>0时,抛物线y=ax2的 2020-12-08 …
二次函数y=ax2+bx+c(a≠0)的图象如下图所示,根据图象回答问题:(1)函数值y有最值为2. 2020-12-13 …