早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,(1)若∠A=30°.求∠NMB的度数;(2)如果将(1)中∠A的度数改为68°,其余条件不变,求∠NMB的度数
题目详情
如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,
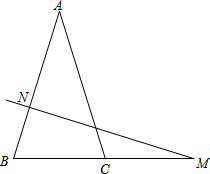
(1)若∠A=30°.求∠NMB的度数;
(2)如果将(1)中∠A的度数改为68°,其余条件不变,求∠NMB的度数;
(3)综合(1)(2),你发现有什么样的规律性,试证明之;
(4)若将(1)中的∠A改为直角或钝角,你发现的规律是否仍然成立?

(1)若∠A=30°.求∠NMB的度数;
(2)如果将(1)中∠A的度数改为68°,其余条件不变,求∠NMB的度数;
(3)综合(1)(2),你发现有什么样的规律性,试证明之;
(4)若将(1)中的∠A改为直角或钝角,你发现的规律是否仍然成立?
▼优质解答
答案和解析
(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=
=90°-
∠A,
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
∠A=15°;
(2)当∠A=68°时,同理仍有∠NMB=
∠A=34°;
(3)规律:∠NMB=
∠A,证明如下:
∵AB=AC,
∴∠B=∠ACB,
∴∠B=
=90°-
∠A,
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
∠A;
(4)当∠A为钝角或直角时,仍然有∠NMB=
∠A.
(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
| 1 |
| 2 |
(2)当∠A=68°时,同理仍有∠NMB=
| 1 |
| 2 |
(3)规律:∠NMB=
| 1 |
| 2 |
∵AB=AC,
∴∠B=∠ACB,
∴∠B=
| 180°-∠A |
| 2 |
| 1 |
| 2 |
∵MN⊥AB,
∴∠BNM=90°,
∴∠NMB=90°-∠B=
| 1 |
| 2 |
(4)当∠A为钝角或直角时,仍然有∠NMB=
| 1 |
| 2 |
看了 如图,在△ABC中,AB=A...的网友还看了以下:
直导线AB通以交变电流i,i的变化规律如 图,若电流的正方向是从A到B,导线AB的右方有不闭合的线 2020-05-14 …
如图,AB线表示晨昏圈的一部分,此时地球公转速度较快.读图回答下列问题:1)此时太阳直射点的地理坐 2020-05-16 …
芳香族化合物X和Y都是从樟脑科植物中提取的香料.X可按如图路线合成Y.已知:①RCH=CHR′①O 2020-06-13 …
如图在△ABC中∠ACB=90°AC=BC=1D是线段AB上的一个动点(不予AB重合)射线AQ⊥在 2020-06-16 …
如图,抛物线y=ax^2+5÷2与直线AB交于点A(1,0)B(4,5÷2)点D是抛物线A,B两点 2020-07-09 …
化合物H是一种香料,存在于金橘中,可用如图路线合成,回答下列问题:(1)11.2L(标准状况)的烃 2020-07-21 …
有机物E是一种医药中间体,可用于制备抗凝血药,可以通过如图路线合成:(1)A可以发生银镜反应,反应的 2020-10-30 …
某研究小组以甲苯为主要原料,采用如图路线合成医药中间体F和Y.已知:①FeHCl②2CH3CHONa 2020-12-14 …
一种用于治疗高血脂的新药灭脂灵(Hepronicate)是按如图路线合成的,已知:①②试回答:(1) 2020-12-22 …
有机物用作印刷油墨的黏合剂,可由如图路线合成(部分反应条件和产物略去):(1)GMA的分子式是;A中 2021-01-06 …