如图，多面体ABCDEF中，DE⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°，四边形BDEF是正方形．（1）求二面角A-EF-C的余弦值；（2）求直线AF与平面ECF所成角的正弦值；（3）在线段EC上是否存在点

Question

如图，多面体ABCDEF中，DE⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°，四边形BDEF是正方形．

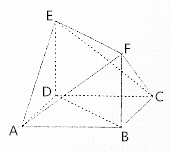
（1）求二面角A-EF-C的余弦值；
（2）求直线AF与平面ECF所成角的正弦值；
（3）在线段EC上是否存在点P，使得AP⊥平面CEF，若存在，求出(EP)/(PC)的值；若不存在，说明理由．

Answer 1

证明：（Ⅰ）取EF的中点O，连接AO，CO，AC．
由题可知：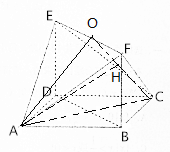
AE=AF=CF=CE=2√(2)，EF=2
所以AO⊥EF，CO⊥EF，则∠AOC为二面角A-EF-C的平面角．
在△AOC中，AC=2√(3)，cos∠AOC=(AO2+CO2-AC2)/(2AO•CO)=(1)/(7)，
故二面角A-EF-C的余弦值为(1)/(7)  …．…..（4分）
（Ⅱ）∵DE⊥平面ABCD，底面ABCD是菱形，四边形BDEF是正方形，
∴DE⊥AC，BD⊥AC，∴AC⊥EF，
∵AE=AF，O是EF中点，∴AO⊥EF，
∵AC∩AO=A，∴EF⊥平面AOC，
∴EF⊂平面CEF，
作AH⊥CO交CO于H点，则AH⊥平面CEF，
∴∠AFH是直线AF与平面ECF所成角，
直线AF与平面ECF所成角的正弦值：
sin∠AFH=(AH)/(AF)=((4√(21))/(7))/(2√(2))=(√(42))/(7)．…．…..（8分）
（Ⅲ）不存在
由第二问知：A在平面CEF上的射影在中线CO上（不在C点），
而过一点作已知平面的垂线只能作一条，
故在线段EC上不存在点P，使得AP⊥平面CEF．…．…..（12分）