抛物线y=-13x2+2x-53与x轴交于A、B，交y轴于点C．（1）直线BC的解析式为．（2）在直线BC上方的抛物线上任取一点P，连接PB，PC，△PBC的面积是否存在最

Question

抛物线y=- (1)/(3)x2+2x- (5)/(3)与x轴交于A、B，交y轴于点C．
（1）直线BC的解析式为___．
（2）在直线BC上方的抛物线上任取一点P，连接PB，PC，△PBC的面积是否存在最大值？存在，求出这个最大值的此时点P的坐标；若不存在，请说明理由．

Answer 1

（1）∵y=-(1)/(3)x2+2x-(5)/(3)=-(1)/(3)（x-1）（x-5），
∴A（1，0），B（5，0）．
令x=0，则y=-(5)/(3)，
∴C（0，-(5)/(3)）．
设直线BC的解析式为y=kx-(5)/(3)（k≠0）．
把点B的坐标代入，得
0=5k-(5)/(3)，
解得k=(1)/(3)，
故直线BC的解析式为：y=(1)/(3)x-(5)/(3)．
故答案是：y=(1)/(3)x-(5)/(3)．

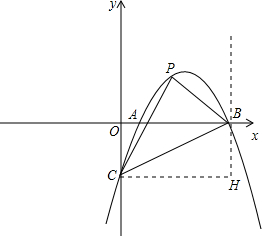
（2）如图，过点B作BH⊥CH，垂足为H．设P（m，-(1)/(3)m²+2m-(5)/(3)）．
S_△PBC=S_△PCH+S_△PHB+S_△BCH，
=(1)/(2)×5×（-(1)/(3)m²+2m-(5)/(3)+(5)/(3)）+(1)/(2)×(5)/(3)×（5-m）-(1)/(2)×5×(5)/(3)，
=-(5)/(6)（m-(5)/(2)）²+(125)/(24)．
所以当m=(5)/(2)时，S_△PBC最大=(125)/(24)．