早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)如图1,若CE=C
题目详情
如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
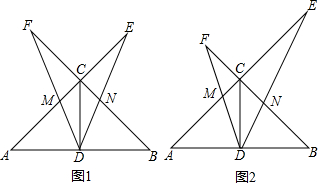
(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.

(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
▼优质解答
答案和解析
 (1)证明:∵∠ACB=90°,AC=BC,AD=BD,
(1)证明:∵∠ACB=90°,AC=BC,AD=BD,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,
∴∠DCE=∠DCF=135°,
在△DCE与△DCF中,
,
∴△DCE≌△DCF,
∴DE=DF;
(2) ①∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°,
∵∠CDF+∠CDE=45°,
∴∠F=∠CDE,
∴△CDF∽△CED,
∴
=
,
即CD2=CE•CF,
∵∠ACB=90°,AC=BC,AD=BD,
∴CD=
AB,
∴AB2=4CE•CF;
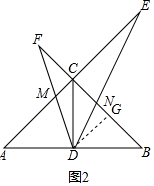
②如图,过D作DG⊥BC于G,
则∠DGN=∠ECN=90°,CG=DG,
当CE=4,CF=2时,
由CD2=CE•CF得CD=2
,
∴在Rt△DCG中,CG=DG=CD•sin∠DCG=2
×sin45°=2,
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△CEN∽△GDN,
∴
=
=2,
∴GN=
CG=
,
∴DN=
=
=
.
 (1)证明:∵∠ACB=90°,AC=BC,AD=BD,
(1)证明:∵∠ACB=90°,AC=BC,AD=BD,∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,
∴∠DCE=∠DCF=135°,
在△DCE与△DCF中,
|
∴△DCE≌△DCF,
∴DE=DF;
(2) ①∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°,
∵∠CDF+∠CDE=45°,
∴∠F=∠CDE,
∴△CDF∽△CED,
∴
| CD |
| CE |
| CF |
| CD |
即CD2=CE•CF,
∵∠ACB=90°,AC=BC,AD=BD,
∴CD=
| 1 |
| 2 |
∴AB2=4CE•CF;
②如图,过D作DG⊥BC于G,
则∠DGN=∠ECN=90°,CG=DG,
当CE=4,CF=2时,
由CD2=CE•CF得CD=2
| 2 |
∴在Rt△DCG中,CG=DG=CD•sin∠DCG=2
| 2 |
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△CEN∽△GDN,
∴
| CN |
| GN |
| CE |
| DG |
∴GN=
| 1 |
| 3 |
| 2 |
| 3 |
∴DN=
| GN2+DG2 |
(
|
2
| ||
| 3 |
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
如图,在平面直角坐标系中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2, 2020-05-16 …
如图直线y=-1/3x+1分别交x轴y轴于A、B两点,三角形AOB绕点O按逆时针方向旋转90度、直 2020-06-15 …
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′ 2020-06-22 …
流星体属于()A.绕地球公转的天体B.绕太阳公转的天体C.绕行星公转的天体D.绕恒星公转的天体 2020-06-25 …
正三角形ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP 2020-07-09 …
观察方格纸上所画图形的位置,并填空.(1)图形B可以看作图形A绕点O顺时针方向旋转得到的;(2)图形 2020-11-03 …
观察细胞质流动的实验中,看到的实验现象是叶绿体()A.绕液泡做定向循环流动B.绕液泡做不定向循环流动 2020-12-15 …
如图,在平面直角坐标系xOy中,正方形ABCD的中点为坐标原点,顶点A的坐标为A(1,1),y轴上一 2020-12-25 …
如图,等边△ABC在直角坐标系xOy中,已知A(2,0),B(-2,0),点C绕点A顺时针方向旋转1 2020-12-25 …
(2014•仙桃)如图,在直角坐标系中,点A的坐标为(-1,2),点C的坐标为(-3,0),将点C绕 2020-12-25 …