早教吧作业答案频道 -->数学-->
如图,在▱ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
题目详情
如图,在▱ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
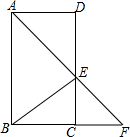
(1)求证:四边形ABCD是矩形;
(2)若AB=14,DE=8,求sin∠AEB的值.

(1)求证:四边形ABCD是矩形;
(2)若AB=14,DE=8,求sin∠AEB的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAF=∠F.
∵∠F=45°,
∴∠DAE=45°.
∵AF是∠BAD的平分线,
∴∠EAB=∠DAE=45°.
∴∠DAB=90°.
又∵四边形ABCD是平行四边形,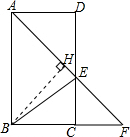
∴四边形ABCD是矩形.
(2) 如图,过点B作BH⊥AE于点H.
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠DCB=∠D=90°.
∵AB=14,DE=8,
∴CE=6.
在Rt△ADE中,∠DAE=45°,
∴∠DEA=∠DAE=45°.
∴AD=DE=8.
∴BC=8.
在Rt△BCE中,由勾股定理得BE=
=10.
在Rt△AHB中,∠HAB=45°,
∴BH=AB•sin45°=7
.
∵在Rt△BHE中,∠BHE=90°,
∴sin∠AEB=
=
.
∴AD∥BC.
∴∠DAF=∠F.
∵∠F=45°,
∴∠DAE=45°.
∵AF是∠BAD的平分线,
∴∠EAB=∠DAE=45°.
∴∠DAB=90°.
又∵四边形ABCD是平行四边形,

∴四边形ABCD是矩形.
(2) 如图,过点B作BH⊥AE于点H.
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠DCB=∠D=90°.
∵AB=14,DE=8,
∴CE=6.
在Rt△ADE中,∠DAE=45°,
∴∠DEA=∠DAE=45°.
∴AD=DE=8.
∴BC=8.
在Rt△BCE中,由勾股定理得BE=
| BC2+CE2 |
在Rt△AHB中,∠HAB=45°,
∴BH=AB•sin45°=7
| 2 |
∵在Rt△BHE中,∠BHE=90°,
∴sin∠AEB=
| BH |
| BE |
7
| ||
| 10 |
看了 如图,在▱ABCD中,∠BA...的网友还看了以下:
基本初等函数,在线等已知x∈[-3,2],求f(x)=(1/4X)-(1/2X)+1的最小和最大值 2020-04-27 …
已知函数f(x)=x的3次方+ax方+x+b,其中a,b属于R(1)若f(x)在x=1处取极小值0 2020-05-23 …
已知函数f(x)=ax+b,当x属于[a1,b1]时,f(x)的值域为[a2,b2],当x属于[a 2020-06-02 …
已知函数f(x)=ax+b,当x属于[a1,b1]时,f(x)的值域为[a2,b2],当x属于[a 2020-06-02 …
关于介值定理..介值定理:设函数f(x)在闭区间[a,b]上连续,f(a)=A,f(b)=B,A≠ 2020-06-03 …
已知函数f(x)=log以2为底(1+x)/(1-x)求证;f(x1)+f(x2)=f[(a+b) 2020-07-15 …
证明:如果函数f(x)在[a,b]上可导,且(f(x)导数的绝对值)小于等于M,则,[(f(b)- 2020-07-16 …
高一指数函数“已知函数f(x)=4^x/4^x+2(1)当实数a>0时,b>0且a+b=1时,求f 2020-08-02 …
求助用matlab解m值(B2/B1+k)*(F1/F2)^m-k*(B3/B2)*(F1/F3)^ 2020-10-31 …
1.已知函数f(x)=x方+2ax+2,x属于-5,5,其最小值为g(a),求g(a)的表达式.2. 2020-11-27 …