早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,已知AB=2,AD=4,点E、F分别在AD、BC上,且AE=1,BF=3,将四边形AEFB沿EF折起,使点B在平面CDEF上的射影H在直线DE上.(1)求证:CD⊥BE;(2)求线段BH的长度;(3)求直线AF
题目详情
如图,在矩形ABCD中,已知AB=2,AD=4,点E、F分别在AD、BC上,且AE=1,BF=3,将四边形AEFB沿EF折起,使点B在平面CDEF上的射影H在直线DE上.
(1)求证:CD⊥BE;
(2)求线段BH的长度;
(3)求直线AF与平面EFCD所成角的正弦值.
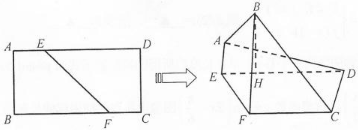 如图,在矩形ABCD中,已知AB=2,AD=4,点E、F分别在AD、BC上,且AE=1,BF=3,将四边形AEFB沿EF折起,使点B在平面CDEF上的射影H在直线DE上.
如图,在矩形ABCD中,已知AB=2,AD=4,点E、F分别在AD、BC上,且AE=1,BF=3,将四边形AEFB沿EF折起,使点B在平面CDEF上的射影H在直线DE上.
(1)求证:CD⊥BE;
(2)求线段BH的长度;
(3)求直线AF与平面EFCD所成角的正弦值.


(1)求证:CD⊥BE;
(2)求线段BH的长度;
(3)求直线AF与平面EFCD所成角的正弦值.
 如图,在矩形ABCD中,已知AB=2,AD=4,点E、F分别在AD、BC上,且AE=1,BF=3,将四边形AEFB沿EF折起,使点B在平面CDEF上的射影H在直线DE上.
如图,在矩形ABCD中,已知AB=2,AD=4,点E、F分别在AD、BC上,且AE=1,BF=3,将四边形AEFB沿EF折起,使点B在平面CDEF上的射影H在直线DE上.(1)求证:CD⊥BE;
(2)求线段BH的长度;
(3)求直线AF与平面EFCD所成角的正弦值.


▼优质解答
答案和解析
(1)证明:由于BH⊥平面CDEF,∴BH⊥CD,又由于CD⊥DE,BH∩DE=H,∴CD⊥平面DBE,∴CD⊥BE.(2) 设BH=h,EH=k,过F作FG垂直ED于点G,因为线段BE,BF在翻折过程中长度不变,根据勾股定理:BE2=BH2+EH2BF2=BH2+FH2...
看了 如图,在矩形ABCD中,已知...的网友还看了以下:
(1.)若N为整数,(2N+1)的平方—(2N-1的平方)能被?整除(2.)1998*6.55+4 2020-04-27 …
因式分解:1、﹙a﹢1﹚的平方﹣﹙a的平方﹢a﹚的平方2、﹙x﹢y﹚的立方﹣9﹙x﹢y﹚的平方3、 2020-05-14 …
1.观察下面几个关于平方和的有趣等式:1的平方+4的平方+6的平方+7的平方=2的平方+3的平方+ 2020-06-04 …
2(4t-1)的平方+5(4t-1)-3x的平方+2xy+y的平方-3x-3y-4a的平方+a-2 2020-06-05 …
1.下列单项式书写不规范的有()(1)3又1/2a的平方b1.下列单项式书写不规范的有()(1)3 2020-06-10 …
帮我解道数学题急在公式(a+1)的平方=a的平方+2a+1中,当a分别取1,2,...,n时,可得 2020-07-09 …
3,-1,6,7,27,(),171,1的平方+2,1的平方-2,2的平方+2,3的平方-2,5的 2020-07-18 …
1-1/22=3/4=(1/2)*(3/2);1-1/32=8/9=(2/3)*(4/3);1-1 2020-07-22 …
1=1的平方1+3=2的平方1+3+5=3的平方1+3+5+7=4的平方1+3+5+7+9=5的平方 2020-11-21 …
观察下列各式1=1的平方-0的平方,3=2的平方-1的平方,5=3的平方-2的平方.你能否得到结论: 2020-12-23 …