早教吧作业答案频道 -->数学-->
如图,已知E是▱ABCD的对角线AC上一点,射线BE与AD交于点F,与CD的延长线交于点G.(1)求证:BE是EF和EG的比例中项;(2)若AF:FD=3:2,求S△ABFS△GBC的值.
题目详情
如图,已知E是▱ABCD的对角线AC上一点,射线BE与AD交于点F,与CD的延长线交于点G.
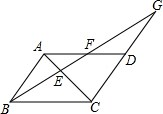
(1)求证:BE是EF和EG的比例中项;
(2)若AF:FD=3:2,求
的值.

(1)求证:BE是EF和EG的比例中项;
(2)若AF:FD=3:2,求
| S△ABF |
| S△GBC |
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABE∽△CGE,△AEF∽△CBE,
∴BE:EG=AE:EC,AE:EC=EF:BE,
∴BE:EG=EF:BE,
∴BE2=EF•EG,
即BE是EF和EG的比例中项;
(2) ∵AD∥BC,AB∥CD,
∴∠AFB=∠CBG,∠ABF=∠G,
∴△ABF∽△CFB,
∵AF:FD=3:2,
∴AF:AD=3:5,
∵AD=BC,
∴AF:BC=3:5,
∴
=
.
∴AB∥CD,AD∥BC,
∴△ABE∽△CGE,△AEF∽△CBE,
∴BE:EG=AE:EC,AE:EC=EF:BE,
∴BE:EG=EF:BE,
∴BE2=EF•EG,
即BE是EF和EG的比例中项;
(2) ∵AD∥BC,AB∥CD,
∴∠AFB=∠CBG,∠ABF=∠G,
∴△ABF∽△CFB,
∵AF:FD=3:2,
∴AF:AD=3:5,
∵AD=BC,
∴AF:BC=3:5,
∴
| S△ABF |
| S△GBC |
| 9 |
| 25 |
看了 如图,已知E是▱ABCD的对...的网友还看了以下:
某有机物A,分子中含两个碳原子,现用A来制取有芳香气味的有机物F和加聚高分子化合物E,其变化如图所 2020-05-14 …
如图,在棱长为a的正方体oabc-o'a'b'c'中,E,F分别是棱AB,BC上的动点,且AE=B 2020-05-16 …
偶函数f(x)=ax2-2bx+1在(-∞,0]上递增,比较f(a-2)与f(b+1)的大小关系( 2020-05-20 …
函数的图象变换用文字说明函数图象间的关系即右边的函数如何通过左边的函数图象变换得到(1)y=f(x 2020-06-03 …
已知偶函数f(x)=loga|x-b|在(-∞,0)上单调递增,则f(a+1)与f(b+2)的大小 2020-06-05 …
已知偶函数f(x)在x∈0,4内单调递增那么a=f(cos120°)与b=f(-π)的大小关系是初 2020-06-06 …
如图甲是一件“马踏飞燕”雕塑(骏马一只蹄稳稳地踏在飞燕上),图乙是马的受力分析图,则()A.G的受 2020-06-27 …
氮化硼(NB)有六方氮化硼和立方氮化硼等不同结构,是一种重要的功能陶瓷材料.请回答下列问题:(1) 2020-07-05 …
逻辑函数F=a异或(a异或b).F的结果? 2020-07-12 …
如图,Rt△ABC中,∠ACB=90°,AC=15,BC=20,将边AC沿CE翻折,使点A落在AB 2020-07-16 …