已知函数f(x)=ax3+bx2+cx+d(a，b，c，d∈R)，且函数f(x)的图象关于原点对称，其图象在x=3的切线方程为8x-y-18=0.(Ⅰ)求f(x)的解析式；(Ⅱ)是否存在区间[a，b]，使得函数g(x)的定义域和值

Question

已知函数f(x)=ax ³ +bx ² +cx+d(a，b，c，d∈R)，且函数f(x)的图象关于原点对称，其图象在x=3的切线方程为8x-y-18=0.

(Ⅰ)求f(x)的解析式；

(Ⅱ)是否存在区间[a，b]，使得函数g(x)的定义域和值域均为[a，b]，且解析式与f(x)的解析式相同？若存在，求出这样的一个区间[a，b]；若不存在，请说明理由.

Answer 1

答案：(Ⅰ)由已知有f(x)是奇函数，所以b=d=0.

又在x=3的切线方程为8x-y-18=0，

所以切点为(3，6)，且f′(x)| _x=3 =8.

而f′(x)=3ax ² +c，所以有

即得a= ，c=-1.故f(x)= x ³ -x.

(Ⅱ)解方程组 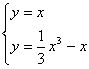，得x ₁ =0，x ₂ = ，x ₃ = ，且f( )= ，f( )= .

又f′(x)=x ² -1，令f′(x)=x ² -1=0，得x=±1.

所以f′(x)在(- ，-1)和(1，+∞)上都有f′(x)＞0，f′(x)在(-1，1)上f′(x)＜0，故f(x)在(-∞，-1)和(1，+∞)上都为增函数，在(-1，1)上为减函数.

所以f(x)在x=1处有极小值 ，在x=-1处有极大值 .

而极小值f(1)= ＞ =f( )，

极大值f(-1)= ＜ =f( )，

所以f(x) _max = ，f(x) _min = .

所以f(x)在区间[ ， ]上的值域为[ ].

综合以上得：存在区间[a，b]=[ ]符合要求.