过抛物线y2=4x的准线与对称轴的交点作直线，交抛物线于M、N两点，问直线的倾斜角的正切值为多少时，以线段MN为直径的圆过抛物线的焦点？

Question

过抛物线 y ² =4 x 的准线与对称轴的交点作直线，交抛物线于 M 、 N 两点，问直线的倾斜角的正切值为多少时，以线段 MN 为直径的圆过抛物线的焦点？

Answer 1

抛物线 y ² =4 x 的准线与对称轴的交点为（-1，0）.设直线 MN 的方程为 y = k （ x +1）.

由 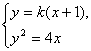得 k ² x ² +2（ k ² -2） x + k ² =0.

∵直线与抛物线交于 M 、 N 两点，

∴Δ=4（ k ² -2） ² -4 k ⁴ ＞0，

即 k ² ＜| k ² -2|.

∴ k ² ＜1，

即-1＜ k ＜1.

设 M （ x ₁ y ₁ ）， N （ x ₂ y ₂ ），抛物线焦点为 F （1，0）.

∵以线段 MN 为直径的圆经过抛物线焦点，

∴ MF ⊥ NF .

∴ =-1，

即 y ₁ y ₂ + x ₁ x ₂ -（ x ₁ + x ₂ ）+1=0.

又 x ₁ + x ₂ =-

x ₁ x ₂ =1 y ₁ ² y ₂ ² =16 x ₁ x ₂ =16且 y ₁ 、 y ₂ 同号，

∴ =-6.

解得 k ² = .∴ k =± .