已知:如图,一次函数y=43x+n与x轴交于点B,一次函数y=-23x+m与y轴交于点C,且它们的图象都经过点D(1,-83).(1)求B、C两点的坐标;(2)设点P(t,0),且t>3,如果△BDP和△CDP的面积
已知:如图,一次函数y=x+n与x轴交于点B,一次函数y=-x+m与y轴交于点C,且它们的图象都经过点D(1,-).
(1)求B、C两点的坐标;
(2)设点P(t,0),且t>3,如果△BDP和△CDP的面积相等,求t的值;
(3)在(2)的条件下,在第四象限内,以CP为腰作等腰Rt△CPQ,求点Q的坐标.
答案和解析
(1)将(1,-
)代入y=x+n,解得n=-4,
即y=x-4,当y=0时,x-4=0.
解得x=3,
即B点坐标为(3,0);
将(1,-)代入y=-x+m,解得n=-2,
即y=-x-2,当x=0时,y=-x-2=-2.
即C点坐标为(0,-2);
(2)连接PC,PD,
如图1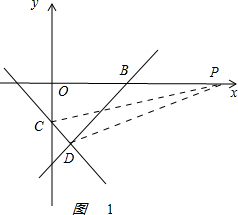 ,
,
S△BDP=(t-3)×|-|=(t-3);
当y=0时,-x-2=0,解得x=-3,即E点坐标为(-3,0).
S△CDP=S△DPE-S△CPE=(t+3)×-×(t+3)×|-2|=(t+3).
由△BDP和△CDP的面积相等,得
(t+3)=(t-3).
解得t=5,
(3)如图2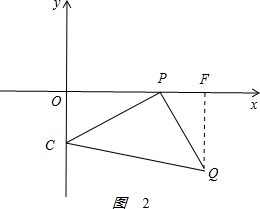 ,
,
QF⊥x轴于F点.
由△CPQ是等腰直角三角形,得
CP=PQ,∠CPQ=90°.
∠OPC+∠PCO=90°,∠OPC+∠QPF=90°,
∴∠PCO=∠QPF.
在△CPO和△PQF中,,
∴△CPO≌△PQF(AAS),
∴PF=OC=2,FQ=OP=5,
Q点的横坐标为5+2=7,Q点的纵坐标为-5,
即Q(7,-5).
在矩形abcd中,bc=3,bg与对角线ac垂直且分别交ac ad及射线cd于点efg ab=x当 2020-05-16 …
已知二次函数 y=x²-(m²+8)x+2(m²+6).(1)求证:不论m取任何实数,此函数图像都 2020-05-16 …
初三几何题.不难已知抛物线y=x平方-(m平方+8)x+2(m平方+6)1.求证:不论M为任何实数 2020-05-20 …
自变量x为何值时,函数y1=x、y2=x-10和y3=40-2x图象上的点都在x轴上方. 2020-06-03 …
自变量x为何值时,函数y1=x、y2=x-10和y3=40-2x图象上的点都在x轴上方. 2020-06-03 …
1.随机变量X的分布列为P{X=k}=a/N,k=1,2,...N求常数a2.设随机变量X只可能取 2020-07-13 …
已知点P(x,y)是圆(x+2)^2+y^2=1上任意一点,1)求x-2y的最大值和最小值,(2)求 2020-10-31 …
已知椭圆方程x^2/16+y^2/9=1,P是椭圆上的任意一点.1)求x+y的取值范围2)l:x+y 2020-11-04 …
初二二次函数已知:抛物线y=x^2-(m-4)x-m问:是否存在实数m,使抛物线与x轴的两个交点都在 2020-12-08 …
初三几何题.不难已知抛物线y=x平方-(m平方+8)x+2(m平方+6)1.求证:不论M为任何实数, 2020-12-23 …


 ,
, ,
, ,
, ,
,