早教吧作业答案频道 -->数学-->
操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;操作二
题目详情
操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.
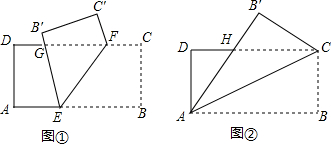
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.

▼优质解答
答案和解析
(1)由折叠的性质可知∠GEF=∠BEF.
∵DC∥AB,
∴∠GFE=∠FEB.
∴∠FEB=∠BEF.
∴EG=FG.
∴△EFG为等腰三角形.
(2)∵四边形ABCD为矩形,
∴AD=BC.
由翻折的性质可知:BC=CB′,∠B′=∠B=90°.
∴AD=CB′,∠D=∠B′.
在△ADH和△CB′H中,
,
∴△ADH≌△CB′H.
∴B′H=DH.
∴△B′HC的周长=B′C+B′H+HC=BC+DH+HC=7.
∵DC∥AB,
∴∠GFE=∠FEB.
∴∠FEB=∠BEF.
∴EG=FG.
∴△EFG为等腰三角形.
(2)∵四边形ABCD为矩形,
∴AD=BC.
由翻折的性质可知:BC=CB′,∠B′=∠B=90°.
∴AD=CB′,∠D=∠B′.
在△ADH和△CB′H中,
|
∴△ADH≌△CB′H.
∴B′H=DH.
∴△B′HC的周长=B′C+B′H+HC=BC+DH+HC=7.
看了 操作与实践:已知长方形纸片A...的网友还看了以下:
根据所示图形填空 已知:线段a,b,且a>2b,画一条线段,使它等于a-2b(1)画射线( );( 2020-05-16 …
a线段比b线段长58,b线段比c线段长32,问a线段比c线段长多少? 2020-06-05 …
已知线段a,b(a〉b)作一条线段使它等于2(a-b)1.用直尺作射线AB,2.用圆规在射线AB上 2020-07-14 …
(2013•东城区二模)定义:P,Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a 2020-07-25 …
北师大版数学八年级下册线段成比例课本第四章第一节上说《四条线段a,b,c,d中,如果a与b的比等于 2020-08-02 …
一道数学题,急`````有三条线段,他们的长分别为a=1cm,b=根号2cm和c=2cm,请再添上 2020-08-02 …
下面的判断是否正确?请说明理由.(1)如果a>b,b≥c,那么a≥c(2)已知线段AB=5cm,线段 2020-11-02 …
填空题)已知线段a,b(a>b),用直尺和圆规画出线段c,使它等于2a-b.(只写出作法)条件:线段 2020-11-06 …
下列各做法中,正确的是()A、以点O为圆心,以任意长为半径画弧,交线段OA于点B.B、以∠AOB的边 2020-11-06 …
已知线段a=0.3m,b=60cm,c=12dm.(1)求线段a与线段b的比.(2)如果线段a、b、 2020-11-28 …