早教吧作业答案频道 -->数学-->
探索研究:已知:△ABC和△CDE都是等边三角形.(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为:,线段AD与BE所成的锐角度数为°;(2)如图2
题目详情
探索研究:已知:△ABC和△CDE都是等边三角形.
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为:___,
线段AD与BE所成的锐角度数为___°;
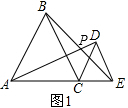
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
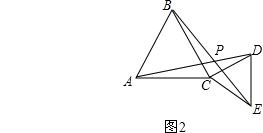
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
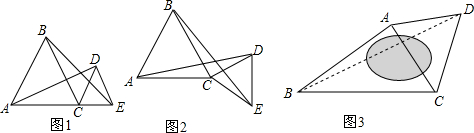
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为:___,
线段AD与BE所成的锐角度数为___°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.

▼优质解答
答案和解析
(1)如图1,
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
由三角形的外角性质,∠DPE=∠PEA+∠DAC,
∠DCE=∠ADC+∠DAC,
∴∠DPE=∠DCE=60°;
故答案为:相等,60;
(2)如图2,
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠BPA=180°-∠ABP-∠BAP=180°-∠ABC-∠BAC=60°.
(3)如图3,以AB为边在△ABC外侧作等边△ABE,连接CE.
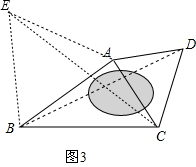
由(2)可得:BD=CE
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形
∵EB=60m BC=80m,
∴CE=
=
=100(m).
∴水池两旁B、D两点之间的距离为100m.

∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
由三角形的外角性质,∠DPE=∠PEA+∠DAC,
∠DCE=∠ADC+∠DAC,
∴∠DPE=∠DCE=60°;
故答案为:相等,60;
(2)如图2,

∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠BPA=180°-∠ABP-∠BAP=180°-∠ABC-∠BAC=60°.
(3)如图3,以AB为边在△ABC外侧作等边△ABE,连接CE.

由(2)可得:BD=CE
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形
∵EB=60m BC=80m,
∴CE=
| BE2+BC2 |
| 602+802 |
∴水池两旁B、D两点之间的距离为100m.
看了 探索研究:已知:△ABC和△...的网友还看了以下:
下列说法中正确的是()A.一条直线和x轴的正方向所成的正角,叫做这条直线的倾斜角B.直线的倾斜角α 2020-04-11 …
一道关于初一全等的几何题,应该不算太难如图,三角形ABC中,角BAC=90,D为三角形内一点,且A 2020-05-13 …
如图所示有一个表面光滑质量很小的截面是等腰三角形的尖劈,其倾角为θ,如图所示,有一个表面光滑、质量 2020-06-28 …
两缝S1和S2之间的距离为d,媒质的折射率为n=1,平行单色光斜入射到双缝上,入射角为θ,如图所示 2020-07-06 …
(2014•大港区二模)如图所示,一束太阳光与水平面成30°角,利用一块平面镜使太阳光竖直射入井中 2020-07-08 …
已知等腰三角形的一腰长为4厘米,一个内角为∠α,如果满足此唯一条件的等腰三角形是唯一的那么∠α需要 2020-07-29 …
已知等腰三角形的一腰长为4厘米,一个内角为∠α,如果满足此唯一条件的等腰三角形是唯一的那么∠α需要 2020-07-29 …
三角函数已知楼房AB高50m,铁塔塔基距楼房房基间水平距离BD为50m,塔高DC为(150+50√3 2020-11-20 …
一条光线在物体表面上发生反射,反射光线与入射光线垂直,则()A.入射角为45°B.入射角为90°C. 2020-12-05 …
等腰三角形abc的顶角为120°,d在bc上,ad=bd,则三角形abd与三角形abc的面积之比为 2020-12-25 …