早教吧作业答案频道 -->数学-->
如图,直线y=ax+b与反比例函数y=mx(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.(1)m=,n=;若M(x1,y1),N(x2,y2)是反比例函数
题目详情
如图,直线y=ax+b与反比例函数y=
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
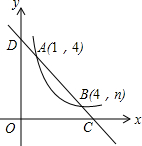
(1)m=___,n=___;若M(x1,y1),N(x2,y2)是反比例函数图象上两点,且0<x1<x2,则y1___y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
| m |
| x |

(1)m=___,n=___;若M(x1,y1),N(x2,y2)是反比例函数图象上两点,且0<x1<x2,则y1___y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
▼优质解答
答案和解析
(1)∵反比例函数y=
(x>0)的图象过点A(1,4),
∴m=1×4=4.
∵点B(4,n)在反比例函数y=
的图象上,
∴m=4n=4,解得:n=1.
∵在反比例函数y=
(x>0)中,m=4>0,
∴反比例函数y=
的图象单调递减,
∵0<x1<x2,
∴y1>y2.
故答案为:4;1;>.
(2)设过C、D点的直线解析式为y=kx+b,
∵直线CD过点A(1,4)、B(4,1)两点,
∴
,解得:
,
∴直线CD的解析式为y=-x+5.
设点P的坐标为(t,-t+5),
∴|t|=|-t+5|,
解得:t=
.
∴点P的坐标为(
,
).
| m |
| x |
∴m=1×4=4.
∵点B(4,n)在反比例函数y=
| 4 |
| x |
∴m=4n=4,解得:n=1.
∵在反比例函数y=
| 4 |
| x |
∴反比例函数y=
| 4 |
| x |
∵0<x1<x2,
∴y1>y2.
故答案为:4;1;>.
(2)设过C、D点的直线解析式为y=kx+b,
∵直线CD过点A(1,4)、B(4,1)两点,
∴
|
|
∴直线CD的解析式为y=-x+5.
设点P的坐标为(t,-t+5),
∴|t|=|-t+5|,
解得:t=
| 5 |
| 2 |
∴点P的坐标为(
| 5 |
| 2 |
| 5 |
| 2 |
看了 如图,直线y=ax+b与反比...的网友还看了以下:
33.14、已知P是抛物线y∧2=2x上的一个动点,过P作圆(x-3) ∧2+y∧2=1的切线,切 2020-05-16 …
直线y=kx(k>0)与双曲线y=x分之2于A,B两点,若A,B两点左边分别是A(x1,y1),B 2020-06-14 …
反比例函数:如图所示,已知双曲线y=x分之k与直线y=4分之1x相交于AB两点,在第一象上的点M( 2020-06-20 …
如图:直线y=-x+18分别与x轴、y轴交于A、B两点;直线y=2x分别与AB交于C点,与过点A且 2020-07-20 …
如图,直线y=三分之四x-4交x轴于点A,交y轴于点B,点D是直线y=三分之四x-4上的一个动点, 2020-08-01 …
如图所示,点P是直线y=x+2与双曲线y=x分之k在第一象限内的一个交点如图,点P是直线y=+2与 2020-08-01 …
一道超级难题,高手的帮忙急!已知抛物线Y=二分之1X平方-2X+1的顶点为P,A为抛物线与Y轴的交 2020-08-02 …
如图,直线y=二分之一x+1分别与x轴、y轴交于点A、B直线y=x+b分别与x轴、y轴交于点C、D直 2020-11-01 …
直线y=-四分之三x+6与x轴、y轴分别交于AB两点,直线y=五分之四x与AB交于C与过A平行于y轴 2020-12-13 …
如图直线y=二分之一x与双曲线y=k除x(k>0,x大于0)交于点A将直线y=二分之一x向上平移四个 2020-12-17 …