早教吧作业答案频道 -->数学-->
如图,椭圆短轴的左右两个端点分别为A,B,直线l:y=kx+1与x轴、y轴分别交于两点E,F,与椭圆交于两点C,D.(Ⅰ)若,求直线l的方程;(Ⅱ)设直线AD,CB的斜率分别为k1,k2,
题目详情
如图,椭圆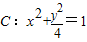 短轴的左右两个端点分别为A,B,直线l:y=kx+1与x轴、y轴分别交于两点E,F,与椭圆交于两点C,D.
短轴的左右两个端点分别为A,B,直线l:y=kx+1与x轴、y轴分别交于两点E,F,与椭圆交于两点C,D.
(Ⅰ)若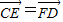 ,求直线l的方程;
,求直线l的方程;
(Ⅱ)设直线AD,CB的斜率分别为k 1 ,k 2 ,若k 1 :k 2 =2:1,求k的值.
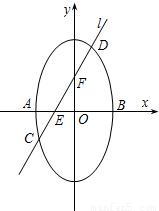
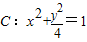 短轴的左右两个端点分别为A,B,直线l:y=kx+1与x轴、y轴分别交于两点E,F,与椭圆交于两点C,D.
短轴的左右两个端点分别为A,B,直线l:y=kx+1与x轴、y轴分别交于两点E,F,与椭圆交于两点C,D.(Ⅰ)若
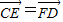 ,求直线l的方程;
,求直线l的方程;(Ⅱ)设直线AD,CB的斜率分别为k 1 ,k 2 ,若k 1 :k 2 =2:1,求k的值.

▼优质解答
答案和解析
分析:
(Ⅰ)设C(x1,y1),D(x2,y2),由得(4+k2)x2+2kx-3=0,再由判别式和根与系数的关系可推导出所求直线l的方程为2x-y+1=0或2x+y-1=0.(Ⅱ)由题设知y12=4(1-x12),y22=4(1-x22),由此推出3x1x2+5(x1+x2)+3=0,所以3k2-10k+3=0,由此可推导出k的值.
(Ⅰ)设C(x1,y1),D(x2,y2),由得(4+k2)x2+2kx-3=0,△=4k2+12(4+k2)=16k2+48,,,(2分)由已知,又,所以(4分)所以,即,(5分)所以,解得k=±2,(6分)符合题意,所以,所求直线l的方程为2x-y+1=0或2x+y-1=0.(7分)(Ⅱ),,k1:k2=2:1,所以,(8分)平方得,(9分)又,所以y12=4(1-x12),同理y22=4(1-x22),代入上式,计算得,即3x1x2+5(x1+x2)+3=0,(12分)所以3k2-10k+3=0,解得k=3或,(13分)因为,x1,x2∈(-1,1),所以y1,y2异号,故舍去,所以k=3.(14分)
点评:
本题考查圆锥曲线的综合运用,是历年高考题的重要题型之一,解题时要注意计算能力的培养,注意积累解题方法.
分析:
(Ⅰ)设C(x1,y1),D(x2,y2),由得(4+k2)x2+2kx-3=0,再由判别式和根与系数的关系可推导出所求直线l的方程为2x-y+1=0或2x+y-1=0.(Ⅱ)由题设知y12=4(1-x12),y22=4(1-x22),由此推出3x1x2+5(x1+x2)+3=0,所以3k2-10k+3=0,由此可推导出k的值.
(Ⅰ)设C(x1,y1),D(x2,y2),由得(4+k2)x2+2kx-3=0,△=4k2+12(4+k2)=16k2+48,,,(2分)由已知,又,所以(4分)所以,即,(5分)所以,解得k=±2,(6分)符合题意,所以,所求直线l的方程为2x-y+1=0或2x+y-1=0.(7分)(Ⅱ),,k1:k2=2:1,所以,(8分)平方得,(9分)又,所以y12=4(1-x12),同理y22=4(1-x22),代入上式,计算得,即3x1x2+5(x1+x2)+3=0,(12分)所以3k2-10k+3=0,解得k=3或,(13分)因为,x1,x2∈(-1,1),所以y1,y2异号,故舍去,所以k=3.(14分)
点评:
本题考查圆锥曲线的综合运用,是历年高考题的重要题型之一,解题时要注意计算能力的培养,注意积累解题方法.
看了 如图,椭圆短轴的左右两个端点...的网友还看了以下:
x^2/a^2+y^2/b^2=1(a>b>0),F1,F2分别为椭圆上的左右焦点,A为椭圆上的上 2020-05-15 …
如图,已知椭圆,F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.( 2020-05-15 …
如图,已知椭圆x2a2+y2b2=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆上的 2020-05-15 …
已知椭圆x^2/a^2+y^2/b^2=1(a>b>0)F1、F2分别为椭圆的左右焦点,A为椭圆的 2020-05-15 …
椭圆ax+by=1(a>0,b>0)与直线x+y=1交于AB两点,M为AB中点,直线OM的斜率为2 2020-05-16 …
已知分别为椭圆的上、下焦点,是抛物线的焦点,点是与在第二象限的交点,且(1)求椭圆的方程;(2)与 2020-06-21 …
已知椭圆的中心在原点O,焦点在x轴上,过其右焦点F做斜率为1的直线l,交椭圆于A、B两点,若椭圆上 2020-06-21 …
如图,已知椭圆x2a2+y2b2=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上 2020-07-20 …
已知椭圆x/8+y/6=1,与圆(x-1)+y=1相切的直线l:y=kx+t交椭圆于M、N两点,若 2020-07-24 …
如图,椭圆=1(a>b>c)的右准线l与x轴的交点为A,椭圆的上顶点为B,过椭圆的右焦点F作垂直于椭 2020-12-01 …