早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.(1)求证:CP=AQ;(2)若BP=1,PQ=22,∠AEF=45°,求矩形ABCD的面积.
题目详情
如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
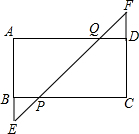
(1)求证:CP=AQ;
(2)若BP=1,PQ=2
,∠AEF=45°,求矩形ABCD的面积.

(1)求证:CP=AQ;
(2)若BP=1,PQ=2
| 2 |
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,
∴∠E=∠F,
∵BE=DF,
∴AE=CF,
在△CFP和△AEQ中,
,
∴△CFP≌△AEQ(ASA),
∴CP=AQ;
(2) ∵AD∥BC,
∴∠PBE=∠A=90°,
∵∠AEF=45°,
∴△BEP、△AEQ是等腰直角三角形,
∴BE=BP=1,AQ=AE,
∴PE=
BP=
,
∴EQ=PE+PQ=
+2
=3
,
∴AQ=AE=3,
∴AB=AE-BE=2,
∵CP=AQ,AD=BC,
∴DQ=BP=1,
∴AD=AQ+DQ=3+1=4,
∴矩形ABCD的面积=AB•AD=2×4=8.
∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,
∴∠E=∠F,
∵BE=DF,
∴AE=CF,
在△CFP和△AEQ中,
|
∴△CFP≌△AEQ(ASA),
∴CP=AQ;
(2) ∵AD∥BC,
∴∠PBE=∠A=90°,
∵∠AEF=45°,
∴△BEP、△AEQ是等腰直角三角形,
∴BE=BP=1,AQ=AE,
∴PE=
| 2 |
| 2 |
∴EQ=PE+PQ=
| 2 |
| 2 |
| 2 |
∴AQ=AE=3,
∴AB=AE-BE=2,
∵CP=AQ,AD=BC,
∴DQ=BP=1,
∴AD=AQ+DQ=3+1=4,
∴矩形ABCD的面积=AB•AD=2×4=8.
看了 如图,矩形ABCD中,延长A...的网友还看了以下:
已知稀溶液中,强酸与强碱反应的中和热的热化学方程式为:H+(aq)+OH-(aq)=H2O(l), 2020-04-08 …
(2009•四川)25℃,101kPa时,强酸与强碱的稀溶液发生中和反应的中和热为57.3kJ/m 2020-04-08 …
25℃,101kPa时,强酸与强碱的稀溶液发生中和反应的中和热为57.3kJ/mol,辛烷的燃烧热 2020-04-08 …
根据右图,可判断出下列离子方程式中错误的是()A.2Ag(s)+Cd2+(aq)=2Ag+(aq) 2020-06-15 …
(2009•镇江一模)下列反应过程中,△H>0且△S>0的是()A.NH3(g)+HCl(g)=N 2020-06-16 …
张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是 2020-07-03 …
(1)依据原电池的构成原理,下列化学反应在理论上可以设计成原电池的是(填序号).A.C(s)+CO 2020-07-03 …
下列热化学方程式书写正确的是(△H的绝对值均为正确值)()A.2NO2═O2+2NO△H=+116 2020-07-19 …
一个数学题过X轴上的动点A(a,0),向抛物线y=x^2+1引两切线,AP,AQ,P,Q为切点,1 2020-07-30 …
下列变化的熵变大于零的是()A.H2O(l)→H2O(g)B.CO2(g)→CO2(s)C.NaOH 2021-02-01 …