早教吧作业答案频道 -->数学-->
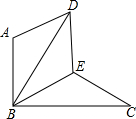
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.(1)求证:△BDE≌△BCE;(2)试判断四边形ABED的形状,并说明理由.
题目详情
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵
,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵
|
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.
看了 如图,△BAD是由△BEC在...的网友还看了以下:
过点P(-3,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是()A.(0, 2020-04-11 …
设函数f(x)=lnx+x+a,若曲线y=e-12sinx+e+12上存在点(x0,y0)使得f( 2020-05-15 …
RT:-27的立方根与√81(根号81)的平方根之和为( ) A.6 B.-6 C.6或-6 D. 2020-05-15 …
巧妙计算.46.3*0.56+5.38*5.6-1+0.056136.24+436.24+736. 2020-05-16 …
氯化钾静滴浓度不得超过( )。 A.0.1%B.0.3%C.0.6%D.0.9%E.1.2% 2020-06-04 …
已知x∈(0,2),关于x的不等式xex<1k+2x-x2恒成立,则实数k的取值范围为()A.[0 2020-07-09 …
已知函数f(x)=exx2-k(2x+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的 2020-07-31 …
已知平面直角坐标系中有四点A(0,0),B(10,0),C(10,6),D(0,6)直线y=mx- 2020-08-02 …
已知平面上四点A(0,0),B(10,0),C10,6),D(0,6)直线Y=mx速求明天有用 2020-10-31 …
某地区人口的出生率为1.2%,死亡率为0.6%,自然增长率是()A.2.1%B.0.3%C.0.6% 2020-11-11 …