早教吧作业答案频道 -->数学-->
如图所示,l1,l2是互相垂直的异面直线,MN是它们的公垂线段,点A,B在直线l1上,且位于M点的两侧,C在l2上,AM=BM=NM=CN(1)求证:异面直线AC与BN垂直;(2)若四面体ABCN的体积VABCN=9,求异
题目详情
如图所示,l1,l2是互相垂直的异面直线,MN是它们的公垂线段,点A,B在直线l1上,且位于M点的两侧,C在l2上,AM=BM=NM=CN
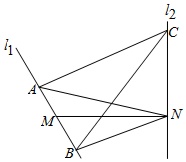
(1)求证:异面直线AC与BN垂直;
(2)若四面体ABCN的体积VABCN=9,求异面直线l1,l2之间的距离.

(1)求证:异面直线AC与BN垂直;
(2)若四面体ABCN的体积VABCN=9,求异面直线l1,l2之间的距离.
▼优质解答
答案和解析
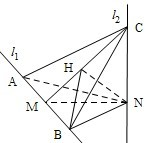 (1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
(1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
由已知MN⊥l1,AM=MB=MN,
可知AN=NB且AN⊥NB.
又AN为AC在平面ABN内的射影.
∴AC⊥NB
(2)∵AM=BM=NM=CN,MN是它们的公垂线段,
就是异面直线l1,l2之间的距离,
由中垂线的性质可得AN=BN,四面体ABCN的体积VABCN=9,
可得:VABCN=9=
×
AB×MN×CN=
MN3,
∴MN=3.
异面直线l1,l2之间的距离为3.
 (1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.
(1)证明:由已知l2⊥MN,l2⊥l1,MN∩l1=M,可得l2⊥平面ABN.由已知MN⊥l1,AM=MB=MN,
可知AN=NB且AN⊥NB.
又AN为AC在平面ABN内的射影.
∴AC⊥NB
(2)∵AM=BM=NM=CN,MN是它们的公垂线段,
就是异面直线l1,l2之间的距离,
由中垂线的性质可得AN=BN,四面体ABCN的体积VABCN=9,
可得:VABCN=9=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴MN=3.
异面直线l1,l2之间的距离为3.
看了 如图所示,l1,l2是互相垂...的网友还看了以下:
正方形ABCD的边CD在正方形ECGF的边CE上,B.C.G三点在一条直线上,切边常为4和6若点m 2020-04-27 …
在直角坐标系中,有一条长度为2的线段AB,点A在y轴上运动,点B在x轴上运动,且保持线段长度不变在 2020-05-16 …
证明四面体每一个顶点与对面重心所连线段共点且这点到顶点的距离是它到对面重心距离的三倍.用向量法证明 2020-05-19 …
根据:两点之间能画一条线段;三点之间能画三条线段;四点之间能画六条线段;五点之间能画十条线段问:N 2020-06-03 …
求c++程序如果一个点在一条线段上(包括这个点是线段端点的情况),我们说“这条线段覆盖了这个点”。 2020-07-04 …
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论:①AB与AC互相垂直②AD与AC 2020-07-29 …
如图所示,下列说法不正确的是()A.点B到AC的垂线段是线段ABB.点C到AB的垂线段是线段ACC 2020-07-29 …
初中几何学过:一条线段是由无数个点组成的.个人推论:可数的线段被分成无数个点,无限的点构成一条有限 2020-07-30 …
直角坐标系中第一象限有一条线段两端点坐标已知同象限内第二条线段两点坐标也已知怎么求第二条线段得端点 2020-08-03 …
一条线段,一头一尾共二个点.若在线段上加一点则有三条线段,加二点有六条线段…接上得到以下规律:线段上 2020-11-27 …