()(本小题满分12分)w.w.w.k.s.5.u.c.o.m如图,直三棱柱ABC-A1B1C1中,AB⊥ACD、E分别为AA1、B1C的中点,DE⊥平面BCC1(Ⅰ)证明:AB=ACw.w.w.k.s.5.u.c.o.m(Ⅱ)
()(本小题满分12分)w.w.w.k.s.5.u.c.o.m ![]()
![]()
如图,直三棱柱ABC-A 1 B 1 C 1 中,AB⊥AC D、E分别为AA 1 、B 1 C的中点,DE⊥平面BCC 1
(Ⅰ)证明:AB=AC w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)设二面角A-BD-C为60° 求B 1 C与平面BCD所成的角的大小
:解法一:(Ⅰ)取BC中点F,连接EF,则EF![]()
![]()
![]() ,从而EF
,从而EF![]() DA.
DA.
连接AF,则ADEF为平行四边形,从而AF//DE.又DE⊥平面![]() ,故AF⊥平面
,故AF⊥平面![]() ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC.
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC.
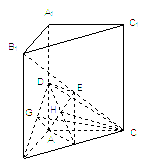 (Ⅱ)作AG⊥BD,垂足为G,连接CG.由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角.由题设知,∠AGC=60 0. .
(Ⅱ)作AG⊥BD,垂足为G,连接CG.由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角.由题设知,∠AGC=60 0. .
设AC=2,则AG=![]() .又AB=2,BC=
.又AB=2,BC=![]() ,故AF=
,故AF=![]() .
.
由![]() 得2AD=
得2AD=![]() ,解得AD=
,解得AD=![]() .
.
故AD=AF.又AD⊥AF,所以四边形ADEF为正方形.
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF.
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD.
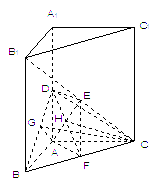 连接CH,则∠ECH为
连接CH,则∠ECH为![]() 与平面BCD所成的角.w.w.w.k.s.5.u.c.o.m
与平面BCD所成的角.w.w.w.k.s.5.u.c.o.m ![]()
![]()
因ADEF为正方形,AD=![]() ,故EH=1,又EC=
,故EH=1,又EC=![]() =2,
=2,
所以∠ECH=30 0 ,即![]() 与平面BCD所成的角为30 0 .
与平面BCD所成的角为30 0 .
解法二:
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A—xyz.
设B(1,0,0),C(0,b,0),D(0,0,c),则![]() (1,0,2c) E(
(1,0,2c) E(![]() ,
,![]() ,c).
,c).
于是![]() =(
=(![]() ,
,![]() ,0),
,0),![]() =(-1,b 0).由DE⊥平面
=(-1,b 0).由DE⊥平面![]() 知DE⊥BC,
知DE⊥BC, ![]() =0,求得b=1,所以 AB=AC.
=0,求得b=1,所以 AB=AC.
(Ⅱ)设平面BCD的法向量![]() 则
则![]() 又
又![]() =(-1,1,
=(-1,1,
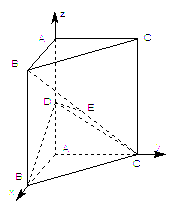
![]() 0),
0),![]() =(-1,0,c) 故
=(-1,0,c) 故
令x=1 则y=1 z=![]()
![]() =(1 1
=(1 1 ![]() ).
).
又平面![]() 的法向量
的法向量![]() =(0,1,0)
=(0,1,0)
由二面角![]() 为60°知,
为60°知,![]() =60°,
=60°,
故 ![]() °,求得
°,求得![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
于是 ![]() ,
, ![]()
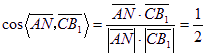 ,
,
![]() °
°
所以![]() 与平面
与平面![]() 所成的角为30°
所成的角为30°
:要证明AB=AC w,,只需证明底边上的中线和底边垂直即可,所以这里要
做辅助线.已知二面角的大小,做题过程要落实,从而找到个棱长的关系,
做二面角的平面角常常利用三垂线定理和逆定理.要证明B 1 C与平面BCD所成
的角,需要找到垂线和垂面.
因为这是一个直棱柱,且AB⊥AC,所以可以建立空间直角坐标系,
利用空间向量证明和求解,常用平面的法向量求线面角.
某化合物A的分子式C8H8O2.A分子中只含一个苯环且苯环上只有一个取代基,实验表明A的分子上有“ 2020-05-02 …
下图是石油分馏塔的示意图,a、b、c三种馏分中 A a的沸点最高 B b的熔点最低 C c的相对分 2020-05-16 …
气象学选择题,求高手,急!话说这些是考试的题目但是没有答案,我自己做了一下,求高手判断是否正确,谢 2020-05-17 …
下列式子中,哪些是分式?哪些是整式?-a的平方分之3b,-3分之a的平方b,x-1分之1,3分之1 2020-06-03 …
先化简再求值:(a+1分之1-a²-1分之a-2)/a+1分之1其中a=梗号下3+1...先化简再 2020-07-06 …
适合下列条件的三角形ABC中,⑴a=3分之1b等于4分之1c=5分之1.适合下列条件的三角形ABC 2020-07-09 …
∫1/a²+x²dx中为什么积分中a的平方提出来后积分的系数是a分之一? 2020-07-27 …
微分中A为什么为其导数!就是那个AΔx+o(x)中的A,书上说A为一个不依赖Δx的常数,那为什么一 2020-07-31 …
先化解,在求值:a²-ab分之a²-b²除以(a+(分开的)a分之2ab+b²)其中a=2,b=-3 2020-11-20 …
西藏被称为“世界屋脊”,其雪域高原迷人的风光和美丽的传说吸引着众多的游人,但有的人常常感到呼吸困难, 2020-12-24 …