早教吧作业答案频道 -->数学-->
求满足下列条件的概率:(1)若mn都是从集合{1,2,3}中任取的数字,求函数f(x)=x2-4mx+4n2有零点的概率;(2)若mn都是从区间[1,4]中任取的数字,在区间[0,4]内任取个实数x,y,求事件“
题目详情
求满足下列条件的概率:
(1)若mn都是从集合{1,2,3}中任取的数字,求函数f(x)=x2-4mx+4n2有零点的概率;
(2)若mn都是从区间[1,4]中任取的数字,在区间[0,4]内任取个实数x,y,求事件“x2+y2>(m-n)2恒成立”的概率.
(1)若mn都是从集合{1,2,3}中任取的数字,求函数f(x)=x2-4mx+4n2有零点的概率;
(2)若mn都是从区间[1,4]中任取的数字,在区间[0,4]内任取个实数x,y,求事件“x2+y2>(m-n)2恒成立”的概率.
▼优质解答
答案和解析
(1)设函数f(x)有零点为事件A,m,n都是从集合{1,2,3}中任取的数字,依题意得
所有的基本事件为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),其中第一个数表示m的取值,第二个数表示n的取值,即基本事件总数为N=9
若函数f(x)=x2-4mx+4n2有零点则△=16m2-16m2≥0,等价于m≥n
事件A所含的基本事件为(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),
则M=6,P(A)=
=
(2)设在区间[0,4]内任取两个实数x,y,“x2+y2>(m-n)2恒成立”为事件C则事件C等价于“x2+y2>9”,(x,y)可以看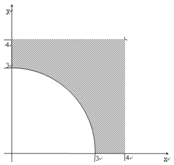 成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},
成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},
而事件B所构成的区域B={(x,y)|x2+y2>9,(x,y)∈Ω}.如图所示(阴影部分表示事件C)
SΩ=4×4=16,SC=16-
,
∴P(C)=
=1-
π
所有的基本事件为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),其中第一个数表示m的取值,第二个数表示n的取值,即基本事件总数为N=9
若函数f(x)=x2-4mx+4n2有零点则△=16m2-16m2≥0,等价于m≥n
事件A所含的基本事件为(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),
则M=6,P(A)=
| 6 |
| 9 |
| 2 |
| 3 |
(2)设在区间[0,4]内任取两个实数x,y,“x2+y2>(m-n)2恒成立”为事件C则事件C等价于“x2+y2>9”,(x,y)可以看
 成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},
成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},而事件B所构成的区域B={(x,y)|x2+y2>9,(x,y)∈Ω}.如图所示(阴影部分表示事件C)
SΩ=4×4=16,SC=16-
| 9π |
| 4 |
∴P(C)=
16-
| ||
| 16 |
| 9 |
| 64 |
看了 求满足下列条件的概率:(1)...的网友还看了以下:
设a∈R,函数f(x)=㏑x-ax一二问可不答重点第3问一定要写(3)若f(x)有两个相异零点x1 2020-07-14 …
若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且|x1|+|x2|=2|k|(k是整数 2020-07-19 …
若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且|x1|+|x2|=2|k|(k是整数 2020-07-19 …
已知x1,x2是一元二次方程(a-6)x2+2ax+a=0的两个实数根.(1)是否存在实数a,使- 2020-07-21 …
(2014•保定一模)已知函数f(x)=3ax2+2bx-a2(a>0),设x1,x2(x1≠x2) 2020-11-12 …
知函数f(x)={1/|x-1|(x≠1),1(x=1)},若关于×的函数h(x)=f(x)^2+b 2020-11-20 …
若函数f(x)=2的x次方+2x-5的零点为x1,g(x)=2log2(x-1)+2x-5的零点为x 2020-12-08 …
已知f(x)=|x2-4|+x2+kx,若f(x)在(0,4)上有两个不同的零点x1,x2,则k的取 2020-12-26 …
已知函数f(x)=2sin(x-派/3)cos(x-派/3)+2根号3cos^2(x-派/3)-根号 2020-12-31 …
若向量a=(x1,y1)向量b=(x2,y2)(1)若x1/x2=y1/y2,则两个向量平行(2)若 2021-02-05 …