早教吧作业答案频道 -->数学-->
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.(Ⅰ)求证:AB1⊥面PBC;(Ⅱ)在BC边上找一点Q,使PQ∥面A1ABB1,并求三棱锥Q-PBB1的体积.
题目详情
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.
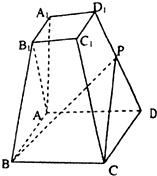
(Ⅰ)求证:AB1⊥面PBC;
(Ⅱ)在BC边上找一点Q,使PQ∥面A1ABB1,并求三棱锥Q-PBB1的体积.

(Ⅰ)求证:AB1⊥面PBC;
(Ⅱ)在BC边上找一点Q,使PQ∥面A1ABB1,并求三棱锥Q-PBB1的体积.
▼优质解答
答案和解析
解(1)取AA1中点M,连结BM,PM,
在PM∥AD∥BC,∴BM⊂平面PBC.
∵AA1⊥面ABCD,BC⊂面ABCD,∴AA1⊥BC,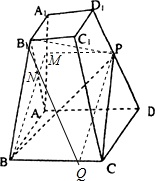
∵ABCD是正方形,∴AB⊥BC,
又AB⊂平面ABB1A1,AA1⊂平面ABB1A1,AB∩AA1=A,
∴BC⊥平面ABB1A1,∵AB1⊂平面ABB1A1,
∴BC⊥AB1.
∵AB=AA1=4,∠BAM=∠B1A1A=90°,AM=B1A1=2,
∴△ABM≌△A1AB1,∴∠MBA=∠B1AA1,
∵∠BAB1+∠B1AA1=90°,∴∠MBA+∠BAB1=90°,
∴BM⊥AB1,
∵BM⊂平面PBC,BC⊂平面PBC,BM∩BC=B,
∴AB1⊥面PBC.
(2)在BC边上取一点Q,使BQ=3,
∵PM为梯形ADD1A1的中位线,A1D1=2,AD=4,
∴PM=3,PM∥AD,又∵BQ∥AD,
∴PM
BQ,
∴四边形PMBQ是平行四边形,
∴PQ∥BM,又BM⊂平面A1ABB1,PQ⊄平面A1ABB1,
∴PQ∥平面A1ABB1.
∵BC⊥平面ABB1A1,BM⊂平面ABB1A1,
∴BQ⊥BM,
∵AB=AA1=4,AM=A1B1=2,∴BM=AB1=2
,
设AB1∩BM=N,则AN=
=
.∴B1N=AB1-AN=
.
∴V B1-BPQ=
S△BPQ•B1N=
×
×3×2
×
=6.
在PM∥AD∥BC,∴BM⊂平面PBC.
∵AA1⊥面ABCD,BC⊂面ABCD,∴AA1⊥BC,

∵ABCD是正方形,∴AB⊥BC,
又AB⊂平面ABB1A1,AA1⊂平面ABB1A1,AB∩AA1=A,
∴BC⊥平面ABB1A1,∵AB1⊂平面ABB1A1,
∴BC⊥AB1.
∵AB=AA1=4,∠BAM=∠B1A1A=90°,AM=B1A1=2,
∴△ABM≌△A1AB1,∴∠MBA=∠B1AA1,
∵∠BAB1+∠B1AA1=90°,∴∠MBA+∠BAB1=90°,
∴BM⊥AB1,
∵BM⊂平面PBC,BC⊂平面PBC,BM∩BC=B,
∴AB1⊥面PBC.
(2)在BC边上取一点Q,使BQ=3,
∵PM为梯形ADD1A1的中位线,A1D1=2,AD=4,
∴PM=3,PM∥AD,又∵BQ∥AD,
∴PM
| ∥ |
. |
∴四边形PMBQ是平行四边形,
∴PQ∥BM,又BM⊂平面A1ABB1,PQ⊄平面A1ABB1,
∴PQ∥平面A1ABB1.
∵BC⊥平面ABB1A1,BM⊂平面ABB1A1,
∴BQ⊥BM,
∵AB=AA1=4,AM=A1B1=2,∴BM=AB1=2
| 5 |
设AB1∩BM=N,则AN=
| AB•AM |
| BM |
4
| ||
| 5 |
6
| ||
| 5 |
∴V B1-BPQ=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
6
| ||
| 5 |
看了 已知四棱台ABCD-A1B1...的网友还看了以下:
下列程序段的输出结果是B.int*p,*q,k=1,j=10;p=&j;q=&k;p=q;(*p) 2020-05-14 …
在高中书上电荷量为—Q一定是表示带负电吗,有没有Q是负数,而—Q是正数所以电荷为正电的可能电荷量为 2020-05-22 …
下面语句中完全正确的是A.inta,*p;*p=&a;B.inta,*p,*q=&a;p=q;C. 2020-06-12 …
在粗糙绝缘的水平面上固定一个带电量为Q的正电荷,已知点电荷周围电场的电势可表示为φ=kQr,式中k 2020-07-01 …
一道高一电学物理题光滑绝缘水平地面上,相隔2L处的A,B两点固定有两个电荷量均为Q的正点电荷,a, 2020-07-22 …
(1)将3p%的硫酸与同体积的p%的硫酸混合得到q%的稀硫酸,则p、q的关系正确的是(填序号,下同 2020-07-29 …
设命题p和命题q,“p∨q”的否定是真命题,则必有()A.p真q真B.p假q假C.p真q假D.p假 2020-08-01 …
Q=(V×D)/(10×A)错误应该是Q×A=V×D×10配制及稀释漂白水时应考虑所使用漂白水之有效 2020-11-06 …
由热值定义可知:热值,式中m是燃料质量,Q是这些燃料完全燃烧放出的热量,那么A热值的大小与Q成正比B 2020-11-29 …
对于命题p和命题q,若p真q假,则命题p∧q和命题p∨q的真假为()A.p∧q和p∨q都为真B.p∧ 2020-12-13 …