早教吧作业答案频道 -->数学-->
如图已知多面体ABCDE中AB⊥平面ACD三角形ACD是正三角形且AD=DE=2AB=1F是CD的中点.(1)求证:AF∥平面BCE;(2)求多面体ABCDE的体积;(3)求二面角C-BE-D的正切值.
题目详情
如图 已知多面体ABCDE中 AB⊥平面ACD 三角形ACD是正三角形 且AD=DE=2 AB=1 F是CD的中点.
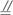
(1)求证:AF∥平面BCE;
(2)求多面体ABCDE的体积;
(3)求二面角C-BE-D的正切值.
▼优质解答
答案和解析
(1)证明:如图 取CE中点M 连结FM、BM 则有FMDEAB ∴四边形AFMB是平行四边形.∴AF∥BM.∵BM平面BCE AF平面BCE ∴AF∥平面BCE.(2)解:由DE⊥平面ACD 则DE⊥AF 又△ACD是等边三角形 则AF⊥CD.而CD∩DE=D 因此AF⊥面CDE.又BM∥AF 则BM⊥平面CDE.VABCDE=VB—ACD+VB—CDE=.(3)解:设G为AD中点 连结CG、BG、EG 则CG⊥AD.由DE⊥平面ACD CG平面ACD 则DE⊥CG 又AD∩DE=D ∴CG⊥平面ADEB.作GH⊥BE于H 连结CH 则CH⊥BE ∴∠CHG为二面角CBED的平面角 由已知AB=1 DE=AD=2 则CG=.∴S△GBE=(1+2)·2-×1×1-×2×1=.易知BE= ∴S△GBE=.∴GH=.∴tan∠CHG=.
看了 如图已知多面体ABCDE中A...的网友还看了以下:
用六种图形如图1,拼成图形如图2:已知图形(1)放在中间一列.①图形(1)应放在A、B、C、D、E 2020-05-17 …
用六种图形如图1,拼成图形如图2:已知图形(1)放在中间一列.①图形(1)应放在A、B、C、D、E 2020-05-17 …
如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2 2020-06-15 …
形如3k-1;4k-1;6k-1有同样形式的素因数证明形如4k-1的素数有无穷多个 2020-07-31 …
某广场用同一种如图所示的地砖拼图案,第一次拼成形如图1所示的图案,第二拼成形如图2所示的图案,第三 2020-08-04 …
一、已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图 2020-11-07 …
一、已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图 2020-11-07 …
如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2, 2020-11-07 …
如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图 2020-12-02 …
已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2, 2020-12-02 …