早教吧作业答案频道 -->数学-->
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且SEEC=SFFD=AGGC.(1)求证:FG∥平面SAB;(2)若平面ABE⊥平面SCD,求多面体SABEF
题目详情
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且
=
=
.
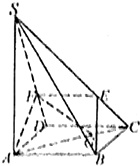
(1)求证:FG∥平面SAB;
(2)若平面ABE⊥平面SCD,求多面体SABEF的体积.
| SE |
| EC |
| SF |
| FD |
| AG |
| GC |

(1)求证:FG∥平面SAB;
(2)若平面ABE⊥平面SCD,求多面体SABEF的体积.
▼优质解答
答案和解析
证明:(1)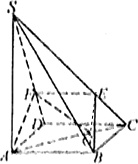 连结EG.
连结EG.
∵
=
,
=
,
∴EG∥SA,EF∥CD,又AB∥CD,
∴EF∥AB,
∵EF⊂平面EFG,EG⊂平面EFG,AB⊂平面SAB,SA⊂平面SAB,EF∩EG=E,SA∩AB=A,
∴平面EFG∥平面SAB.
∵FG⊂平面EFG,
∴FG∥平面SAB.
(2)∵SA⊥平面ABCD,AB⊂平面ABCD,
∴SA⊥AB,又AD⊥AB,AD∩SA=A,SA⊂平面SAD,AD⊂平面SAD,
∴AB⊥平面SAD,
∵EF∥AB,
∴EF⊥平面SAD,
∵SF⊂平面SAD,AF⊂平面SAD,
∴EF⊥AF,EF⊥SF,
∵平面ABE⊥平面SCD,平面ABE∩平面SCD=EF,SF⊂平面SCD,
∴SF⊥平面ABEF.
∵AB=CD=AD=4,∠SDA=60°,
∴DF=2,AF=2
,SD=8,
∴SF=6.
∵
=
=
,
∴EF=3.
∴VS-ABEF=
S梯形ABEF•SF=
×
×(3+4)×2
×6=14
.
 连结EG.
连结EG.∵
| SE |
| EC |
| AG |
| GC |
| SF |
| FD |
| SE |
| EC |
∴EG∥SA,EF∥CD,又AB∥CD,
∴EF∥AB,
∵EF⊂平面EFG,EG⊂平面EFG,AB⊂平面SAB,SA⊂平面SAB,EF∩EG=E,SA∩AB=A,
∴平面EFG∥平面SAB.
∵FG⊂平面EFG,
∴FG∥平面SAB.
(2)∵SA⊥平面ABCD,AB⊂平面ABCD,
∴SA⊥AB,又AD⊥AB,AD∩SA=A,SA⊂平面SAD,AD⊂平面SAD,
∴AB⊥平面SAD,
∵EF∥AB,
∴EF⊥平面SAD,
∵SF⊂平面SAD,AF⊂平面SAD,
∴EF⊥AF,EF⊥SF,
∵平面ABE⊥平面SCD,平面ABE∩平面SCD=EF,SF⊂平面SCD,
∴SF⊥平面ABEF.
∵AB=CD=AD=4,∠SDA=60°,
∴DF=2,AF=2
| 3 |
∴SF=6.
∵
| EF |
| CD |
| SF |
| SD |
| 3 |
| 4 |
∴EF=3.
∴VS-ABEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
看了 如图所示,四棱锥S-ABCD...的网友还看了以下:
一个长方形篮球场,长A米,宽B米它的长比宽多C米,周长为D米,面积为E平方米.现给出几个数:86, 2020-05-04 …
已知无限长均匀带电直线上电荷线密度(即单位长度所带的电荷量)为λ,则与直线相距为d处的电场强度为E 2020-05-13 …
特殊位置的圆的一般方程设法例如与x轴相切时的定义域为E≠0,D^2-4F=0咋么理解 2020-06-25 …
SQL计算列的问题我要在数据库中加入计算列,比如有a,b,c三列,计算列D=(a+b+c)/3,然 2020-07-10 …
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,AF为△ABC的角平分线,分别过点C、B作 2020-07-12 …
(2012•西藏)如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,A 2020-07-26 …
如图,已知P是等边△ABC的BC边上任意一点,过P点分别作AB、AC的垂线PE、PD,垂足为E、D 2020-07-29 …
如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧上一点,连接BD,AD,OC,∠ADB=3 2020-07-31 …
如图,在△ABC中,∠C=90°,CA=4,CB=3.GH与CA延长线、AB、CB延长线相切,切点 2020-08-01 …
质子和中子都是由u夸克和d夸克组成,u夸克带电量为e,d夸克带电量为e,e为基元电荷。下列论断可能正 2020-12-24 …