早教吧作业答案频道 -->数学-->
如图，在梯形ABCD中，AD∥BC，CE⊥AB于E，△BDC为等腰直角三角形，∠BDC=90°，BD=CD，CE与BD交于F，连接AF，求证：CF=AB+AF．
题目详情
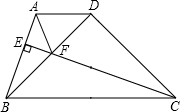如图，在梯形ABCD中，AD∥BC，CE⊥AB于E，△BDC为等腰直角三角形，∠BDC=90°，BD=CD，CE与BD交于F，连接AF，求证：CF=AB+AF．
如图，在梯形ABCD中，AD∥BC，CE⊥AB于E，△BDC为等腰直角三角形，∠BDC=90°，BD=CD，CE与BD交于F，连接AF，求证：CF=AB+AF．
如图，在梯形ABCD中，AD∥BC，CE⊥AB于E，△BDC为等腰直角三角形，∠BDC=90°，BD=CD，CE与BD交于F，连接AF，求证：CF=AB+AF．▼优质解答
答案和解析
证明：作DH⊥AD交CE于H，如图，∵AD∥BC，∴DH⊥BC，∵△BDC为等腰直角三角形，∴∠3=45°，BD=CD，∴∠4=45°，∴∠3=∠4=∠CDH，∵CE⊥AB，∴∠2+∠BFE=90°，而∠1+∠DFC=90°，∠BFE=∠CFD，∴∠1=∠2，在△CDH...
看了 如图，在梯形ABCD中，AD...的网友还看了以下：
已知a/b=c/d=e/f=2,当b+d≠0时,a+c/b+d=；当b+d+f≠0时,a+c+e/ 2020-05-14 …
已知a,b,c,d,e,f六个数.如果a/b=c/d=e/f（b+d+f≠0）,那么a+c+e/b 2020-06-02 …
若a/b=c/d=e/f,则下列各式中正确的是（）.A.e/f=ac/bdB.e/f=(a+c+e 2020-06-06 …
如图，若AB∥CD，则∠B、∠C、∠E三者之间的关系是（）A．∠B+∠C+∠E=180°B．∠B+ 2020-06-12 …
（1）如图①∵∠B+∠D+∠1=180°又∵∠1=∠A+∠2∠2=∠C+∠E∴∠A+∠C+∠E+∠ 2020-06-13 …
A、B、C、D、E、F六个小朋友做游戏，每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小 2020-06-22 …
A、B、C、D、E、F六个小朋友做游戏，每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小 2020-07-01 …
急一道数学题已知a/b=c/d=e/f=m/n（b+d+f+...+n≠0）（1）试说明：a+c+e 2020-11-01 …
A，B，C，D，E，F六个足球队进行单循环赛，当比赛进行到某一天时，统计出A，B，C，D，E五队已分 2021-01-09 …
A，B，C，D，E，F六个足球队进行单循环赛，当比赛进行到某一天时，统计出A，B，C，D，E五队已分 2021-01-09 …