早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.(1)求证:△BFH≌△DEG;(2)连接DF,若BF=DF,判断四边形EGFH是什么特殊四边形
题目详情
如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.
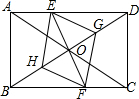
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,判断四边形EGFH是什么特殊四边形?并证明你的结论.如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.

(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,判断四边形EGFH是什么特殊四边形?并证明你的结论.


(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,判断四边形EGFH是什么特殊四边形?并证明你的结论.如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH、FG.

(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,判断四边形EGFH是什么特殊四边形?并证明你的结论.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
,
∴BFH≌△DEG(AAS);
(2)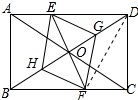 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:
连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
∠FBH=∠EDG ∠BHF=∠DGE BF=DE ∠FBH=∠EDG ∠FBH=∠EDG ∠FBH=∠EDG ∠BHF=∠DGE ∠BHF=∠DGE ∠BHF=∠DGE BF=DE BF=DE BF=DE
∴BFH≌△DEG(AAS);
(2) 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:
连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
∴AD∥BC,AD=BC,OB=OD,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
|
∴BFH≌△DEG(AAS);
(2)
 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
|
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
∴BFH≌△DEG(AAS);
(2)
 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
看了 如图,在矩形ABCD中,点E...的网友还看了以下:
数学 排列组合问题甲乙丙丁四人参加一项特殊的接力赛 ,比赛要求有五次交接棒,但不要求每人都参加,只 2020-05-16 …
在实验室中用二氧化锰跟浓盐酸反应制备干燥纯净的氯气.进行此实验,所用仪器如图:(1)连接上述仪器的 2020-05-17 …
已知△BCE、△DCF分别是以平行四边形ABCD的邻边BC、CD为边向外所作的等边三角形求证:△A 2020-05-17 …
20世纪初,英法和解后,德国更感到英俄对抗的特殊价值,德国首相皮洛说,所有希望都系于他们相信英俄正 2020-05-17 …
定积分求导f(t)=sint/t在t=0时不存在,F(x)=f(t)dt在0到x上的定积分。那么F 2020-07-11 …
体温计里的水银在测量体温后为什么会在细管处断开?“体温表的构造很特殊,在玻璃泡和细管相接的地方,有一 2020-11-08 …
(2005•常州)如图所示,为使滑动变阻器的滑片P向右移动时,通电螺线管对条形磁铁的斥力变大,则电源 2020-11-12 …
如图所示,一个小球从某一高度下落,在接触轻质弹簧并压缩弹簧竖直向下运动的过程中,当小球速度达到最大时 2020-12-01 …
在光滑的水平面上,质量分别为m1和m2的木块,A和B之间用轻弹簧相连,在拉力F的作用下,以加速度a做 2021-01-22 …
如图所示,接触面光滑的A、B两物体质量分别为m和2m,由劲度系数为K的轻弹簧连接,在力F作用下,沿光 2021-01-23 …