数学活动：将形状不同的三张矩形纸片按照如图的方式折叠，BE、DF分别是折痕．折叠后点A、C分别落在矩形对角线BD上的点P、点Q处．（1）如图1，折叠后的四边形BEDF是什么四边形？请说明理

Question

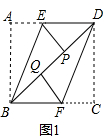
数学活动：将形状不同的三张矩形纸片按照如图的方式折叠，BE、DF分别是折痕．折叠后点A、C分别落在矩形对角线BD上的点P、点Q处．
（1）如图1，折叠后的四边形BEDF是什么四边形？请说明理由．
（2）如图2，折叠后若点P与点Q重合，则矩形ABCD中 (BC)/(AB)的值是___（直接写答案）．
（3）如图3，延长 EP交BC边于点G，延长 FQ交AD边于点H，若四边形EGFH是菱形，AD=10，求矩形的宽AB的长．


(BC)/(AB)的值是___（直接写答案）．
（3）如图3，延长 EP交BC边于点G，延长 FQ交AD边于点H，若四边形EGFH是菱形，AD=10，求矩形的宽AB的长．
(BC)/(AB) BC AB BC BC AB AB

Answer 1

（1）如图1，
∵AB∥CD，
∴∠ABD=∠CDB，
由折叠的性质可知，∠EBD=∠ABE=(1)/(2)∠ABD，∠FDB=∠CDF=(1)/(2)∠CDB，
∴∠EBD=∠FDB，
∴EB∥DF，又DE∥BF，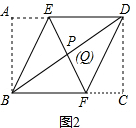
∴折叠后的四边形BEDF是平行四边形；

（2）如图2，∵DC=DP，BA=BP，DC=BA，
∴CD=(1)/(2)BD，又∠C=90°，
∴∠DBC=30°，
∴(BC)/(AB)=√(3)，
故答案为：√(3)；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²+10²=（3x）²，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． (1)/(2)12111222∠ABD，∠FDB=∠CDF=(1)/(2)∠CDB，
∴∠EBD=∠FDB，
∴EB∥DF，又DE∥BF，
∴折叠后的四边形BEDF是平行四边形；

（2）如图2，∵DC=DP，BA=BP，DC=BA，
∴CD=(1)/(2)BD，又∠C=90°，
∴∠DBC=30°，
∴(BC)/(AB)=√(3)，
故答案为：√(3)；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²+10²=（3x）²，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． (1)/(2)12111222∠CDB，
∴∠EBD=∠FDB，
∴EB∥DF，又DE∥BF，
∴折叠后的四边形BEDF是平行四边形；

（2）如图2，∵DC=DP，BA=BP，DC=BA，
∴CD=(1)/(2)BD，又∠C=90°，
∴∠DBC=30°，
∴(BC)/(AB)=√(3)，
故答案为：√(3)；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²+10²=（3x）²，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． (1)/(2)12111222BD，又∠C=90°，
∴∠DBC=30°，
∴(BC)/(AB)=√(3)，
故答案为：√(3)；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²+10²=（3x）²，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． (BC)/(AB)BCABBCBCBCABABAB=√(3)，
故答案为：√(3)；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²+10²=（3x）²，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． √(3)

3

3

33，
故答案为：√(3)；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²+10²=（3x）²，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． √(3)

3

3

33；

（3）如图3，∵AB=PB，CD=QD，EP⊥BD，FQ⊥DQ，
∴PQ是菱形EGFH的高，即EH与GF间的距离为PQ，
故PQ=AB=CD，
∴BD=BP+PQ+QD=AB+AB+AB，
∴3AB=BD，
∴设AB=x，则BD=3x，
∵AD=10，
∴x²2+10²2=（3x）²2，
解得：x=±(5√(2))/(2)（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． (5√(2))/(2)5√(2)25√(2)5√(2)5√(2)

2

2

22222（负数舍去），
即矩形的宽AB的长为：(5√(2))/(2)． (5√(2))/(2)5√(2)25√(2)5√(2)5√(2)

2

2

22222．