早教吧作业答案频道 -->数学-->
已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.(1)求证:△BFH≌△DEG;(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四
题目详情
已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
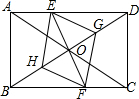
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.


(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
,
∴BFH≌△DEG(AAS);
(2)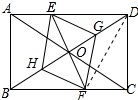 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:
连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
∠FBH=∠EDG ∠BHF=∠DGE BF=DE ∠FBH=∠EDG ∠FBH=∠EDG ∠FBH=∠EDG ∠BHF=∠DGE ∠BHF=∠DGE ∠BHF=∠DGE BF=DE BF=DE BF=DE
∴BFH≌△DEG(AAS);
(2) 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:
连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
∴AD∥BC,AD=BC,OB=OD,
∴∠FBH=∠EDG,
∵AE=CF,
∴BF=DE,
∵EG∥FH,
∴∠OHF=∠OGE,
∴∠BHF=∠DGE,
在△BFH和△DEG中,
|
∴BFH≌△DEG(AAS);
(2)
 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
|
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
| ∠FBH=∠EDG | |
| ∠BHF=∠DGE | |
| BF=DE |
∴BFH≌△DEG(AAS);
(2)
 四边形EGFH是菱形;理由如下:
四边形EGFH是菱形;理由如下:连接DF,如图所示:
由(1)得:BFH≌△DEG,
∴FH=EG,
又∵EG∥FH,
∴四边形EGFH是平行四边形,
∵BF=DF,OB=OD,
∴EF⊥BD,
∴EF⊥GH,
∴四边形EGFH是菱形.
看了 已知:如图,在矩形ABCD中...的网友还看了以下:
在C.G.S单位制中,是如何定义磁通势的单位吉伯(Gilbert)的?急用是定义,不是1吉伯等于0 2020-04-25 …
质量为m的小球,自A点有静止开始沿半径为R的1/4光滑圆周滚下,到达B点后进入粗糙水平面,最后停在 2020-05-13 …
如图所示,一点光源位于凸透镜的主轴上,凸透镜位置固定.当点光源位于A点时,它的像在B点;当点光源位 2020-05-16 …
关于凸透镜成像规律的题目:把烛焰放在A点时,成像在B点;当把烛焰放在B点时,成像在C点,则凸透镜的 2020-06-21 …
已知等腰三角形ABC,AB=AC=5,BC=8,把三角形ABC绕点B旋转,使得点A落在直线BC上A 2020-06-25 …
为什么群的中心是群呢?因为首先1属于C(G),因为1能与群中任何元素交换;其次,如果x属于C(G), 2020-11-03 …
直线Y=-2X+10与X轴,Y轴分别交于A,B两点,把三角形AOB沿AB翻折,点oO落在C处,则点C 2020-11-03 …
非空集合G关于运算⊕满足:(1)对任意a、b∈G,都有a⊕b∈G;(2)存在c∈G,使得对一切a∈G 2020-11-10 …
根音的问题百科原话:俗称的“分数和弦”,“分子”是根音,“分母”是最低音,C/G则是C为根音G为最低 2020-11-21 …
e.s.u.在c.g.s.单位制里是什么意思?和g,cm,s是什么关系?电子的电量是4.80e-10 2021-02-05 …