已知抛物线y2=8x的准线与双曲线x2a2-y216=1相交于A，B两点，点F为抛物线的焦点，△ABF为直角三角形，则双曲线的离心率为（）A.3B.2C.6D.3
已知抛物线y2=8x的准线与双曲线
-x2 a2
=1相交于A，B两点，点F为抛物线的焦点，△ABF为直角三角形，则双曲线的离心率为（ ）y2 16
A. 3
B. 2
C. 6
D. 3
已知抛物线y2=8x的准线与双曲线
-x2 a2
=1相交于A，B两点，点F为抛物线的焦点，△ABF为直角三角形，则双曲线的离心率为（ ）y2 16
| x2 |
| a2 |
| y2 |
| 16 |
| x2 |
| a2 |
| y2 |
| 16 |
| x2 |
| a2 |
| y2 |
| 16 |
A. 3
B. 2
C. 6
| 6 |
| 6 |
D. 3
| 3 |
| 3 |
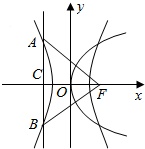依题意知抛物线的准线x=-2，代入双曲线方程得y=±
| 4 |
| a |
| 4-a2 |
| 4 |
| a |
| 4-a2 |
∵△FAB是等腰直角三角形，∴
| 4 |
| a |
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 4 |
| a |
| 4-a2 |
| 4 |
| a |
| 4-a2 |
∵△FAB是等腰直角三角形，∴
| 4 |
| a |
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 4-a2 |
| 4 |
| a |
| 4-a2 |
∵△FAB是等腰直角三角形，∴
| 4 |
| a |
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 4 |
| a |
| 4-a2 |
∵△FAB是等腰直角三角形，∴
| 4 |
| a |
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 4-a2 |
∵△FAB是等腰直角三角形，∴
| 4 |
| a |
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 4 |
| a |
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 4-a2 |
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| 2 |
∴双曲线的离心率为e=
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| c |
| a |
| ||
| a |
| ||
|
故选：A．
| ||
| a |
| a2+16 |
| a2+16 |
| a2+16 |
| a2+16 |
| ||
|
故选：A．
| ||
|
| 18 |
| 2 |
| 18 |
| 18 |
| 18 |
| 2 |
| 2 |
| 2 |
故选：A．
1.a≠0,b≠0,则a/|a|＋b/|b|的不同取值的个数为（）A.3B.2C.1D.02.若|x 2020-03-31 …
基本不等式超费解130已知a>b>0,求a2+1/（a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
写出合适下列条件的椭圆的标准方程(1)a=4,焦点为F1(-3,0);F2(3,0)(2)a=4, 2020-05-16 …
θ是第三象限角，方程x2+y2sinθ=cosθ表示的曲线是（）A.焦点在y轴上的双曲线B.焦点在 2020-05-21 …
假设集合A满足以下条件：诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
双酚A是食品、饮料包装和奶瓶等塑料制品的添加剂，能导致人体内分泌失调，对儿童的健康危害更大．下列有 2020-07-19 …
长期吸烟容易患肺癌的原因是（）A.煤焦油粘于肺泡壁，使肺泡失去弹性B.煤焦油能导致机体产生原癌基因C 2020-12-07 …
某草原生态系统的一条食物链A→B→C中，各种群对能量的同化、利用、传递等数量关系如表（单位：百万千焦 2020-12-21 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …