早教吧作业答案频道 -->数学-->
求乘积的展开式的项数．
题目详情
求乘积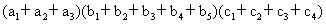 
的展开式的项数．
求乘积 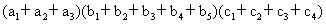的展开式的项数．
求乘积 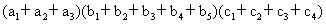的展开式的项数．
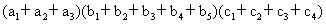的展开式的项数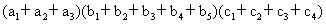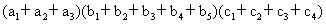． 的展开式的项数．▼优质解答
答案和解析
解析：
解析：
由多项式乘法法则可知，乘积的展开式，即先将多项式的每一项与的每一项分别相乘，显然，展开后没有同类项可合并，然后再把这两个多项式的展开式的每一项与的每一项分别相乘，从而得到其展开式，其中，，，…均为其展开式的项．因此要确定其展开式的项数，则只需要依次确定乘积的下标m、n、k的值即可，而m可取1，2，3；n可取1，2，3，4，5；k可取1，2，3，4．由分步乘法计数原理可知，所求的项数为3×5×4=60．
答案：60
解析：
解析：
由多项式乘法法则可知，乘积的展开式，即先将多项式的每一项与的每一项分别相乘，显然，展开后没有同类项可合并，然后再把这两个多项式的展开式的每一项与的每一项分别相乘，从而得到其展开式，其中，，，…均为其展开式的项．因此要确定其展开式的项数，则只需要依次确定乘积的下标m、n、k的值即可，而m可取1，2，3；n可取1，2，3，4，5；k可取1，2，3，4．由分步乘法计数原理可知，所求的项数为3×5×4=60．
答案：60解析：
解析：
由多项式乘法法则可知，乘积的展开式，即先将多项式的每一项与的每一项分别相乘，显然，展开后没有同类项可合并，然后再把这两个多项式的展开式的每一项与的每一项分别相乘，从而得到其展开式，其中，，，…均为其展开式的项．因此要确定其展开式的项数，则只需要依次确定乘积的下标m、n、k的值即可，而m可取1，2，3；n可取1，2，3，4，5；k可取1，2，3，4．由分步乘法计数原理可知，所求的项数为3×5×4=60．
解析：
解析：
由多项式乘法法则可知，乘积的展开式，即先将多项式的每一项与的每一项分别相乘，显然，展开后没有同类项可合并，然后再把这两个多项式的展开式的每一项与的每一项分别相乘，从而得到其展开式，其中，，，…均为其展开式的项．因此要确定其展开式的项数，则只需要依次确定乘积的下标m、n、k的值即可，而m可取1，2，3；n可取1，2，3，4，5；k可取1，2，3，4．由分步乘法计数原理可知，所求的项数为3×5×4=60．
看了 求乘积的展开式的项数．...的网友还看了以下：
整式的乘法：（1）单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变 2020-05-13 …
看图列式．（1）乘加算式：乘减算式：（2）乘加算式：乘减算式：． 2020-05-13 …
一个乘数是0.8，积与另一个乘数的和是36，求被乘数．列式是[]A．36×0.8B．36÷0.8C 2020-05-15 …
excel当e2小于10则乘2大于等于10小于20乘1.5大于等于30乘1.4 求公式excel当 2020-05-16 …
已知多项式x2-mx-n与x-2的乘积中不含x2项和x项，求这两个多项式的乘积． 2020-07-27 …
已知被除式是x3+3x2-1，商式是x，余式是-1，求除式． 2020-07-31 …
已知被除式是x3+3x2-1，商式是x，余式是-1，求除式． 2020-07-31 …
下列说法完整且正确的是（）A．同底数幂相乘，指数相加B．幂的乘方，等于指数相乘C．积的乘方，等于把 2020-08-01 …
整式的乘法：（1）单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变 2020-08-03 …
1.利用换底公式求下式的值:log225乘log34乘log592.利用换底公式证明:logab乘l 2021-01-01 …
相关搜索：求乘积的展开式的项数．