早教吧作业答案频道 -->数学-->
如图，分别以△ABC的三边为边，在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR，连接PA，AQ，QR，RP，那么四边形PRQA是平行四边形吗？证明你的结论．
题目详情
如图，分别以△ABC的三边为边，在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR，连接PA，AQ，QR，RP，那么四边形PRQA是平行四边形吗？证明你的结论．
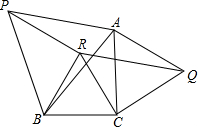如图，分别以△ABC的三边为边，在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR，连接PA，AQ，QR，RP，那么四边形PRQA是平行四边形吗？证明你的结论．
如图，分别以△ABC的三边为边，在BC的同侧向外作等边△ABP、等边△ACQ、等边△BCR，连接PA，AQ，QR，RP，那么四边形PRQA是平行四边形吗？证明你的结论．▼优质解答
答案和解析
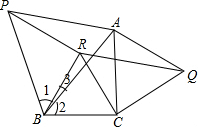四边形PRQA是平行四边形，
理由：∵△ABP，△BCR都是等边三角形，
∴∠PBA=∠RBC=60°，AB=PB，BC=RB，
∴∠1=∠2=60°-∠ABE，
在△ABC和△PRB中，
，
∴△ABC≌△PBR（SAS）．
∴PR=AC．
∵△ACQ是等边三角形，
∴AC=AQ，
∴DE=AF．
同理可得AP=QR．
∴四边形PRQA是平行四边形．
PB=AB ∠1=∠2 RB=BC PB=AB PB=AB PB=AB∠1=∠2 ∠1=∠2 ∠1=∠2RB=BC RB=BC RB=BC
∴△ABC≌△PBR（SAS）．
∴PR=AC．
∵△ACQ是等边三角形，
∴AC=AQ，
∴DE=AF．
同理可得AP=QR．
∴四边形PRQA是平行四边形．
四边形PRQA是平行四边形，理由：∵△ABP，△BCR都是等边三角形，
∴∠PBA=∠RBC=60°，AB=PB，BC=RB，
∴∠1=∠2=60°-∠ABE，
在△ABC和△PRB中，
|
∴△ABC≌△PBR（SAS）．
∴PR=AC．
∵△ACQ是等边三角形，
∴AC=AQ，
∴DE=AF．
同理可得AP=QR．
∴四边形PRQA是平行四边形．
|
| PB=AB |
| ∠1=∠2 |
| RB=BC |
| PB=AB |
| ∠1=∠2 |
| RB=BC |
| PB=AB |
| ∠1=∠2 |
| RB=BC |
| PB=AB |
| ∠1=∠2 |
| RB=BC |
∴△ABC≌△PBR（SAS）．
∴PR=AC．
∵△ACQ是等边三角形，
∴AC=AQ，
∴DE=AF．
同理可得AP=QR．
∴四边形PRQA是平行四边形．
看了 如图，分别以△ABC的三边为...的网友还看了以下：
指出下列各组条件与结论中,条件p是结论q的什么条件.（1） p：a＞2,b＞3,q：a+b＞5；（ 2020-05-14 …
已知p^2-p-1=0,1-q-q^2=0,且pq不等于1.则pq+1/q1-q-q^2=0因为q 2020-06-07 …
指出下列各组条件中,条件p是结论q的什么条件(1)p:ab>o,q:/a/>/b/(4)p:整数a 2020-06-12 …
关于充要条件的概念.“已知命题p和q,如果p能推出q,那么p是q的充分条件,q是p的必要条件；如果 2020-06-27 …
函数求利润的疑惑某厂的总收益函数和总成本函数分别为：R(Q)=18QC(Q)=Q^3-9Q^2+3 2020-07-16 …
人们使用四万只象鼻虫和它们的215磅粪便物，历经30多年时间弄清了棉子象鼻虫的四种信息素的组成，它 2020-07-19 …
离散数学中环算几条边K4有几边几面构造下面推理证明(1)前提：┑(p∧q),┑q∧r,┑r结论：┑ 2020-07-30 …
四个班进行比赛,小明猜想的比赛结果是:三班第一名,二班第二名,一班第一名,四班第四名.小化猜想的名次 2020-12-06 …
四个班进行比赛,小明猜想的比赛结果是:三班第一名,二班第二名,一班第一名,四班第四名.小化猜想的名次 2020-12-25 …
1.对角线相等的四边形是矩形.2.三角形不是多边形.3.对角线互相垂直且有一组邻边相等的四边形是菱形 2021-02-01 …