早教吧作业答案频道 -->数学-->
在△ABC中,AB=BC,BD⊥AC于点D.(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F.①求证:△BEF是等腰三角形;②求证:BD=12(BC+BF);(2)点E在AB边上,连接CE.若BD=12(BC+BE
题目详情
在△ABC中,AB=BC,BD⊥AC于点D.
(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F.
①求证:△BEF是等腰三角形;
②求证:BD=
(BC+BF);
(2)点E在AB边上,连接CE.若BD=
(BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路.
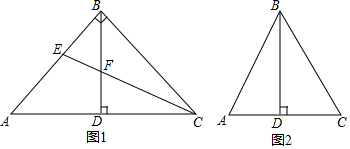
(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F.
①求证:△BEF是等腰三角形;
②求证:BD=
| 1 |
| 2 |
(2)点E在AB边上,连接CE.若BD=
| 1 |
| 2 |

▼优质解答
答案和解析
 (1)①在△ABC中,AB=BC,BD⊥AC于点D,
(1)①在△ABC中,AB=BC,BD⊥AC于点D,
∴∠ABD=∠CBD,AD=CD,
∵∠ABC=90°,
∴∠ACB=45°,
∵CE平分∠ACB,
∴∠ECB=∠ACE=22.5°,
∴∠BEF=∠CFD=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形;
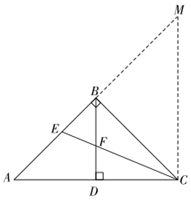
②如图,延长AB至M,使得BM=AB,连接CM,
∴BD∥CM,BD=
CM,
∴∠BCM=∠DBC=∠ABD=∠BMC=45°,
∠BFE=∠MCE,
∴BC=BM,
由①得,∠BEF=∠BFE,BE=BF,
∴∠BFE=∠MCE=∠BEF,
∴EM=MC,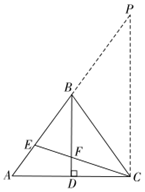
∴BD=
EM=
(BC+BF);
(2)∠ACE=
∠ABC.
求解∠ACE与∠ABC关系的思路:
a,延长AB至P,使得BP=AB,连接CP,与(1)②同理可得BD∥PC,BD=
PC,BP=BC;
b,由BD=
(BC+BE),可证明△PEC和△BEF分别是等腰三角形;
c,由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得
=90°-∠DCF,即可证明∠ACE=
∠ABC.
 (1)①在△ABC中,AB=BC,BD⊥AC于点D,
(1)①在△ABC中,AB=BC,BD⊥AC于点D,∴∠ABD=∠CBD,AD=CD,
∵∠ABC=90°,
∴∠ACB=45°,
∵CE平分∠ACB,
∴∠ECB=∠ACE=22.5°,
∴∠BEF=∠CFD=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形;
②如图,延长AB至M,使得BM=AB,连接CM,
∴BD∥CM,BD=
| 1 |
| 2 |
∴∠BCM=∠DBC=∠ABD=∠BMC=45°,
∠BFE=∠MCE,
∴BC=BM,
由①得,∠BEF=∠BFE,BE=BF,
∴∠BFE=∠MCE=∠BEF,
∴EM=MC,

∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∠ACE=
| 1 |
| 4 |
求解∠ACE与∠ABC关系的思路:
a,延长AB至P,使得BP=AB,连接CP,与(1)②同理可得BD∥PC,BD=
| 1 |
| 2 |
b,由BD=
| 1 |
| 2 |
c,由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得
| 180°-∠EBF |
| 2 |
| 1 |
| 4 |
看了 在△ABC中,AB=BC,B...的网友还看了以下:
已知,如图∠A=∠C,CD丄AB于D,交AE于F,试断定ΔAEB的形状,并说明你的结论的合理性.AD 2020-03-30 …
一个函数连续,一个函数不连续,那么这两个函数的商连续吗答案是不连续.设f(x)是连续的,F(x)是 2020-05-16 …
如果一元函数f(x0,y)在y0处连续,f(x,y0)在x0处连续,那么二元函数f(x,y)在点( 2020-05-21 …
数学分析题》》关于连续的设f:D->实数,|f|:D->实数因为|f|(x)=|f(x)|举一个例 2020-06-03 …
一道高数函数连续性的问题!谢谢!设f(x)在x0连续,g(x)在x0不连续,则在x0处()A.f( 2020-06-06 …
1.设f(x)在[0,1]上连续,且f(0)=f(1),证明:存在x0∈[0,1],使得f(x0) 2020-06-18 …
f(x)在x=x0连续,g(u)在u=u0=f(x0)不连续,则g(f(x))在x=x0不连续,该 2020-07-13 …
设函数f(x)定义在[a,b]上,下面命题正确的是f(x)可导,则f(x)连续f(x)不可导,则f 2020-07-16 …
谁能给解释下复合函数连续性的问题?f(x)在x=x0处连续.g(x)在这点不连续.请问f(x)+g 2020-08-02 …
1函数f[x]在xo处可导,则|f[x]|在xo处A必定可导B必定不可导C必定连续D必定不连续2函数 2020-11-20 …