早教吧作业答案频道 -->数学-->
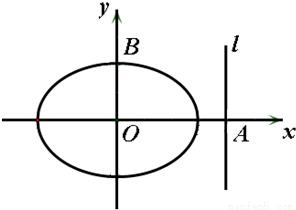
已知椭圆E:的离心率为,且过点,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为.(1)求椭圆E的方程及圆O的方程;(2)若M
题目详情
已知椭圆E: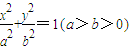 的离心率为
的离心率为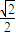 ,且过点
,且过点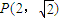 ,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为
,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为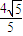 .
.
(1)求椭圆E的方程及圆O的方程;
(2)若M是准线l上纵坐标为t的点,求证:存在一个异于M的点Q,对于圆O上任意一点N,有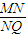 为定值;且当M在直线l上运动时,点Q在一个定圆上.
为定值;且当M在直线l上运动时,点Q在一个定圆上.
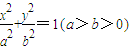 的离心率为
的离心率为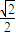 ,且过点
,且过点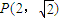 ,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为
,设椭圆的右准线l与x轴的交点为A,椭圆的上顶点为B,直线AB被以原点为圆心的圆O所截得的弦长为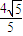 .
.(1)求椭圆E的方程及圆O的方程;
(2)若M是准线l上纵坐标为t的点,求证:存在一个异于M的点Q,对于圆O上任意一点N,有
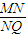 为定值;且当M在直线l上运动时,点Q在一个定圆上.
为定值;且当M在直线l上运动时,点Q在一个定圆上.
▼优质解答
答案和解析
【答案】分析:(1)由椭圆E的离心率为,知a=2k,c=,b2=2k2,即椭圆E:,把点代入得k2=2,由此能求出椭圆E方程和圆的方程.(2)椭圆E的右准线l的方程为x=4.设l上取定的点M为(4,t),圆O上任意的一点N为(x0,y0),定点Q为(x,y).因为NM与NQ的比是常数且Q不同于M,所以NQ2=λNM2,λ是正的常数(λ≠1),即(x0-x)2+(y0-y)2=λ(x0-4)2+λ(y0-t)2,即x2 0+y2 0-2xx0-2yy0+x2+y2=λ(x2 0+y2 0+16+t2-8x0-2ty0).由此入手能够导出点Q在圆心,0,半径为的定圆上.定值为:,Q在圆心,半径为的定圆上.(1)∵椭圆E:的离心率为,∴a=2k,c=,b2=2k2,∴椭圆E:,把点代入得k2=2,∴椭圆E方程:.圆的方程:x2+y2=4(2)证明:椭圆E的右准线l的方程为x=4. 设l上取定的点M为(4,t),圆O上任意的一点N为(x0,y0),定点Q为(x,y). 因为NM与NQ的比是常数且Q不同于M,所以NQ2=λNM2,λ是正的常数(λ≠1),即(x0-x)2+(y0-y)2=λ(x0-4)2+λ(y0-t)2,即x2 0+y2 0-2xx0-2yy0+x2+y2=λ(x2 0+y2 0+16+t2-8x0-2ty0). 将x2 0+y2 0=4代入,有-2xx0-2yy0+x2+y2+4=-8λx0-2λty0+(20+t2)λ. 又有无数组(x0,y0),从而x=4λ,①y=tλ,②x2+y2+4=(20+t2)λ.③ 由①②代入③,得16λ2+t2λ2+4=(20+t2)λ,即(16+t2)λ2-(20+t2)λ+4=0,所以(λ-1)[(16+t2)λ-4]=0. 又因为λ≠1,所以λ=,即存在一个定点Q(不同于点M),使得对于圆O上的任意一点N,均有为定值. 将16+t2=代入③,得x2+y2+4=+4λ,即x2+y2=4λ,于是x2+y2=x,即x-2+y2=,故点Q在圆心,0,半径为的定圆上.定值为:,Q在圆心,半径为的定圆上点评:本题考查圆与圆锥曲线的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件.
看了 已知椭圆E:的离心率为,且过...的网友还看了以下:
已知椭圆方程为:x^2+y^2/8=1.(1)是否存在实数k,直线y=kx+2交椭圆于P、Q两点, 2020-05-15 …
已知圆心C在x轴上的圆过点A(2,2)和B(4,0).(1)求圆C的方程;(2)求过点M(4,6) 2020-06-09 …
已知椭圆x^2/a^2+y^2/b^2=1(a>b>0)与X轴的正方向交于A,0为坐标原点,以OA 2020-06-29 …
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B 2020-07-11 …
如图,O是以原点为圆心,半径为2的圆,点A(6,2),点P是O上一动点,以线段PA为斜边构造直角△ 2020-07-19 …
如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O 2020-07-21 …
在平面直角坐标系中,以原点O为圆心的圆过点A(0,35),直线y=kx-3k+4与⊙O交于B、C两 2020-07-21 …
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线与⊙O交于B、C两点,则弦BC 2020-07-26 …
(2014•东海县二模)如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+6上的一点,过 2020-07-30 …
椭圆的离心率求解已知椭圆x^2/a^2+y^2/b^2=1(a>b>0)的右焦点为F1,左焦点为F2 2021-01-04 …