如图，已知平行六面体ABCD—A1B1C1D1的底面是菱形且∠C1CB=∠C1CD=∠BCD=60°(1)证明C1C⊥BD；(2)假定CD=2，CC1=，记面C1BD为α面CBD为β

Question

如图，已知平行六面体 ABCD — A ₁ B ₁ C ₁ D ₁ 的底面是菱形且∠ C ₁ CB =∠ C ₁ CD =∠ BCD =60°

 (1)证明   C ₁ C ⊥ BD ；

(2)假定 CD =2， CC ₁ = ，记面 C ₁ BD 为 α 面 CBD 为 β 求二面角 α — BD — β 的平面角的余弦值；

 (3)当 的值为多少时，可使 A ₁ C ⊥面 C ₁ BD ？

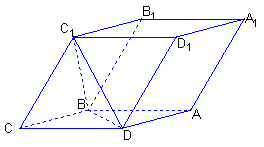
如图，已知平行六面体 ABCD — A ₁ B ₁ C ₁ D ₁ 的底面是菱形且∠ C ₁ CB =∠ C ₁ CD =∠ BCD =60°

 (1)证明   C ₁ C ⊥ BD ；

(2)假定 CD =2， CC ₁ = ，记面 C ₁ BD 为 α 面 CBD 为 β 求二面角 α — BD — β 的平面角的余弦值；

 (3)当 的值为多少时，可使 A ₁ C ⊥面 C ₁ BD ？

如图，已知平行六面体 ABCD — A ₁ B ₁ C ₁ D ₁ 的底面是菱形且∠ C ₁ CB =∠ C ₁ CD =∠ BCD =60°

ABCD A ₁ B ₁ C ₁ D ₁ C ₁ CB C ₁ CD BCD

 (1)证明   C ₁ C ⊥ BD ；

C ₁ C BD

(2)假定 CD =2， CC ₁ = ，记面 C ₁ BD 为 α 面 CBD 为 β 求二面角 α — BD — β 的平面角的余弦值；

CD CC ₁ C ₁ BD α CBD β α BD β

 (3)当 的值为多少时，可使 A ₁ C ⊥面 C ₁ BD ？

A ₁ C C ₁ BD

Answer 1

(1)证明   连结 A ₁ C ₁ 、 AC ， AC 和 BD 交于点 O ，连结 C ₁ O ，

∵四边形 ABCD 是菱形，∴ AC ⊥ BD ， BC = CD

又∵∠ BCC ₁ =∠ DCC ₁ ， C ₁ C 是公共边，∴△ C ₁ BC ≌△ C ₁ DC ，∴ C ₁ B = C ₁ D

∵ DO = OB ，∴ C ₁ O ⊥ BD ，但 AC ⊥ BD ， AC ∩ C ₁ O = O

∴ BD ⊥平面 AC ₁ ，又 C ₁ C 平面 AC ₁ ，∴ C ₁ C ⊥ BD  

 (2)解   由(1)知 AC ⊥ BD ， C ₁ O ⊥ BD ，

∴∠ C ₁ OC 是二面角 α — BD — β 的平面角  

在△ C ₁ BC 中， BC =2， C ₁ C = ，∠ BCC ₁ =60°，

∴ C ₁ B ² =2 ² +( ) ² －2×2× ×cos60°=  

∵∠ OCB =30° ∴ OB = BC =1 C ₁ O = 即 C ₁ O = C ₁ C  

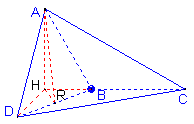
作 C ₁ H ⊥ OC ，垂足为 H ，则 H 是 OC 中点且 OH = ，∴cos C ₁ OC =

(3)解   由(1)知 BD ⊥平面 AC ₁ ，∵ A ₁ O 平面 AC ₁ ，∴ BD ⊥ A ₁ C ，当 =1时，平行六面体的六个面是全等的菱形，同理可证 BC ₁ ⊥ A ₁ C ，又∵ BD ∩ BC ₁ = B ，∴ A ₁ C ⊥平面 C ₁ BD  

解析:

见详解

(1)证明   连结 A ₁ C ₁ 、 AC ， AC 和 BD 交于点 O ，连结 C ₁ O ，

(1)证明   连结 A A ₁ 1 C C ₁ 1 、 AC AC ， AC AC 和 BD BD 交于点 O O ，连结 C C ₁ 1 O O ，

∵四边形 ABCD 是菱形，∴ AC ⊥ BD ， BC = CD

∵四边形 ABCD ABCD 是菱形，∴ AC AC ⊥ BD BD ， BC BC = CD CD

又∵∠ BCC ₁ =∠ DCC ₁ ， C ₁ C 是公共边，∴△ C ₁ BC ≌△ C ₁ DC ，∴ C ₁ B = C ₁ D

又∵∠ BCC BCC ₁ 1 =∠ DCC DCC ₁ 1 ， C C ₁ 1 C C 是公共边，∴△ C C ₁ 1 BC BC ≌△ C C ₁ 1 DC DC ，∴ C C ₁ 1 B B = C C ₁ 1 D D

∵ DO = OB ，∴ C ₁ O ⊥ BD ，但 AC ⊥ BD ， AC ∩ C ₁ O = O

∵ DO DO = OB OB ，∴ C C ₁ 1 O O ⊥ BD BD ，但 AC AC ⊥ BD BD ， AC AC ∩ C C ₁ 1 O O = O O

∴ BD ⊥平面 AC ₁ ，又 C ₁ C 平面 AC ₁ ，∴ C ₁ C ⊥ BD  

∴ BD BD ⊥平面 AC AC ₁ 1 ，又 C C ₁ 1 C C 平面 AC AC ₁ 1 ，∴ C C ₁ 1 C C ⊥ BD BD  

 (2)解   由(1)知 AC ⊥ BD ， C ₁ O ⊥ BD ，

 (2)解   由(1)知 AC AC ⊥ BD BD ， C C ₁ 1 O O ⊥ BD BD ，

∴∠ C ₁ OC 是二面角 α — BD — β 的平面角  

∴∠ C C ₁ 1 OC OC 是二面角 α α — BD BD — β β 的平面角  

在△ C ₁ BC 中， BC =2， C ₁ C = ，∠ BCC ₁ =60°，

在△ C C ₁ 1 BC BC 中， BC BC =2， C C ₁ 1 C C = ，∠ BCC BCC ₁ 1 =60°，

∴ C ₁ B ² =2 ² +( ) ² －2×2× ×cos60°=  

∴ C C ₁ 1 B B ² 2 =2 ² 2 +( ) ² 2 －2×2× ×cos60°=  

∵∠ OCB =30° ∴ OB = BC =1 C ₁ O = 即 C ₁ O = C ₁ C  

∵∠ OCB OCB =30° ∴ OB OB = BC BC =1 C C ₁ 1 O O = 即 C C ₁ 1 O O = C C ₁ 1 C C  

作 C ₁ H ⊥ OC ，垂足为 H ，则 H 是 OC 中点且 OH = ，∴cos C ₁ OC =

作 C C ₁ 1 H H ⊥ OC OC ，垂足为 H H ，则 H H 是 OC OC 中点且 OH OH = ，∴cos C C ₁ 1 OC OC =

(3)解   由(1)知 BD ⊥平面 AC ₁ ，∵ A ₁ O 平面 AC ₁ ，∴ BD ⊥ A ₁ C ，当 =1时，平行六面体的六个面是全等的菱形，同理可证 BC ₁ ⊥ A ₁ C ，又∵ BD ∩ BC ₁ = B ，∴ A ₁ C ⊥平面 C ₁ BD  

(3)解   由(1)知 BD BD ⊥平面 AC AC ₁ 1 ，∵ A A ₁ 1 O O 平面 AC AC ₁ 1 ，∴ BD BD ⊥ A A ₁ 1 C C ，当 =1时，平行六面体的六个面是全等的菱形，同理可证 BC BC ₁ 1 ⊥ A A ₁ 1 C C ，又∵ BD BD ∩ BC BC ₁ 1 = B B ，∴ A A ₁ 1 C C ⊥平面 C C ₁ 1 BD BD   解析:

见详解

见详解