早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.(Ⅰ)若点M是线段AC的中点,证明:(1)MB∥平面AEF;(2)平面AEF⊥平
题目详情
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
(Ⅰ)若点M是线段AC的中点,证明:
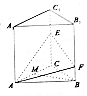
(1)MB∥平面AEF;
(2)平面AEF⊥平面ACC1A1;
(Ⅱ)求三棱锥B-AEF的体积.
(Ⅰ)若点M是线段AC的中点,证明:

(1)MB∥平面AEF;
(2)平面AEF⊥平面ACC1A1;
(Ⅱ)求三棱锥B-AEF的体积.
▼优质解答
答案和解析
(Ⅰ)证明:(1)取线段AE的中点G,连结MG,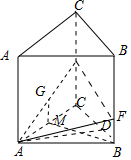
则MG=
EC=BF,又MG∥EC∥BF,
∴MBFG是平行四边形,故MB∥FG.
而FG⊂平面AEF,MB⊄平面AEF,
∴MB∥平面AEF;
(2)∵MB⊥AC,平面ACC1A1⊥平面ABC,
∴MB⊥平面ACC1A1,而BM∥FG,
∴FG⊥平面ACC1A1.
∵FG⊂平面AEF,∴平面AEF⊥平面ACC1A1;
(Ⅱ) 作AD⊥BC于D,则AD⊥平面BEF,且AD=
.
于是VA-BEF=
×S△BEF×AD=
×
×1×2×
=
.
故VB-AEF=VA-BEF=
.

则MG=
| 1 |
| 2 |
∴MBFG是平行四边形,故MB∥FG.
而FG⊂平面AEF,MB⊄平面AEF,
∴MB∥平面AEF;
(2)∵MB⊥AC,平面ACC1A1⊥平面ABC,
∴MB⊥平面ACC1A1,而BM∥FG,
∴FG⊥平面ACC1A1.
∵FG⊂平面AEF,∴平面AEF⊥平面ACC1A1;
(Ⅱ) 作AD⊥BC于D,则AD⊥平面BEF,且AD=
| 3 |
于是VA-BEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
故VB-AEF=VA-BEF=
| ||
| 3 |
看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
高二物理·光的折射如图所示,一束激光从O点由空气射入厚度均匀的介质,经下表面反射后,从上表面的A点如 2020-03-31 …
一质点沿一边长为2m的正方形轨道运动每秒移动1m初始位置为A点如图2-5所示.分别求下列情况下的路 2020-05-13 …
8、(2011绵阳)已知抛物线y=x2-2x+m-1与x轴只有一个交点,且与y轴交于A点,如图,设 2020-05-16 …
:已知△ABC,AB=20,AC=12,B点以3/s的速度朝BA方向前进,A点以2/S的速度朝AC 2020-05-16 …
若从A点看B点是北偏东60度,则从B点看A点如何? 2020-06-02 …
在下面给出的数轴中A表示1,B表示-2.5,回答下面的问题:(1)A、B之间的距离是(2)观察数轴 2020-07-30 …
abc三个人一起去一家咖啡馆就餐a点了1杯咖啡,1个蛋糕花了7.20$b点了2杯咖啡,2个蛋糕,3 2020-08-04 …
以知两直线I1,I2相交于A点(2,3),I1经过点(-1,1),I2经过点(1/2,-1).请写出 2020-11-01 …
求人做这几道初一数学题1:定义一种新运算.a☆b=a/b-a+b,如2☆3=2/3-2+3.计算4☆ 2020-11-18 …
(1/2)水平传送带AB以v=200m/s的速度匀速运动,如图所示,A、B相距0.011Km.一物体 2020-12-12 …