如图所示，折线B0A1B2A2B3A3…中线段分别平行于x轴或y轴，A1，A2，…，An…这些点在函数y=2x-1（x>1）图象上，B1，B2…Bn…这些点在直线y=x上，设点An的纵坐标为yn．（1）用yn表示yn+1（n∈N*）

Question

如图所示，折线B₀A₁B₂A₂B₃A₃…中线段分别平行于x轴或y轴，A₁，A₂，…，A_n…这些点在函数y=(2)/(x-1)（x>1）图象上，B₁，B₂…B_n…这些点在直线y=x上，设点A_n的纵坐标为y_n．

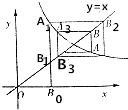
（1）用y_n表示y_n+1（n∈N^*）；
（2）若B₀（(11)/(5)，0），请写出数列{y_n}的所有项；
（3）设B₀（x₀，0），当x₀为何值时，数列{y_n}是一个无穷的常数列．

Answer 1

（1）设B₀（x₀，0），由题意可得B₁（x₀，x₀），
A₁（x₀，(2)/(x0-1)），B₂（(2)/(x0-1)，(2)/(x0-1)），
A₂（(2)/(x0-1)，(2)/((2)/(x0-1)-1)），
B₃（(2)/((2)/(x0-1)-1)，(2)/((2)/(x0-1)-1)），
…
即有y_n+1=f（y_n）=(2)/(yn-1)（y_n>1）；
（2）由B₀（(11)/(5)，0），
可得数列{y_n}的所有项为：(11)/(5)，(5)/(3)，3，1；
（3）设B₀（x₀，0），由（1）可得，
令y_n+1=y_n=t，（t>1），
即有t=(2)/(t-1)，即为t²-t-2=0，
解得t=2（-1舍去）．
则x₀为2时，数列{y_n}是一个无穷的常数列．