早教吧作业答案频道 -->数学-->
如图,已知抛物线y=ax2+52x+c经过A(4,0),B(1,0)两点,(1)求该抛物线的解析式;(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA
题目详情
如图,已知抛物线y=ax2+
x+c经过A(4,0),B(1,0)两点,
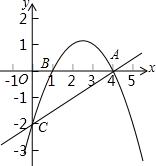
(1)求该抛物线的解析式;
(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.
| 5 |
| 2 |
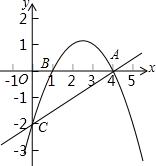
(1)求该抛物线的解析式;
(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.
▼优质解答
答案和解析
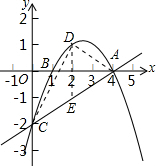 (1)把A(4,0),B(1,0)代入抛物线的解析式得:
(1)把A(4,0),B(1,0)代入抛物线的解析式得:
,
解得:
,
则抛物线解析式为y=-
x2+
x-2;
(2)存在,理由如下:
设D的横坐标为t(0<t<4),则D点的纵坐标为-
t2+
t-2,
过D作y轴的平行线交AC于E,连接CD,AD,如图所示,
由题意可求得直线AC的解析式为y=
x-2,
∴E点的坐标为(t,
t-2),
∴DE=-
t2+
t-2-(
t-2)=-
t2+2t,
∴△DAC的面积S=
×(-
t2+2t)×4=-t2+4t=-(t-2)2+4,
当t=2时,S最大=4,
∴此时D(2,1),△DAC面积的最大值为4.
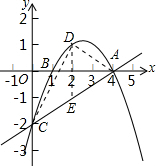 (1)把A(4,0),B(1,0)代入抛物线的解析式得:
(1)把A(4,0),B(1,0)代入抛物线的解析式得:
|
解得:
|
则抛物线解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)存在,理由如下:
设D的横坐标为t(0<t<4),则D点的纵坐标为-
| 1 |
| 2 |
| 5 |
| 2 |
过D作y轴的平行线交AC于E,连接CD,AD,如图所示,
由题意可求得直线AC的解析式为y=
| 1 |
| 2 |
∴E点的坐标为(t,
| 1 |
| 2 |
∴DE=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△DAC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
当t=2时,S最大=4,
∴此时D(2,1),△DAC面积的最大值为4.
看了 如图,已知抛物线y=ax2+...的网友还看了以下:
长方形的面积公式咋么换算成平方米打比方1米*1米的方怎么换算平方米最好说的详细点 2020-05-13 …
面向对象与Java程序设计基础题目:设计一个程序可以一计算平面图形的面积和立体图形的体积。1.使用 2020-05-17 …
这个java习题,如何比较任意两个长方形的面积,用数组?java新手,弄了半天没弄全,------ 2020-05-17 …
把一根长1米的方木横截成相等的四根后,表面积比原来增加236平方厘米,这根方木原来的体积是多少立方 2020-05-21 …
一段长1米的方钢,横截面是边长5厘米的正方形,这段方钢的体积是(),表面积是(). 2020-05-23 …
特殊的方法求特殊四边形面积的方法比如说对角线相互垂直的四边形面积等于二分之一对角线乘积不要那种平行 2020-06-02 …
编写一个程序计算三角形、正方形和圆形三种图形的面积.依题意,可以抽象出一个基类base,在其中说明 2020-06-06 …
空间向量的面积问题1,a=(1,1,1)b=(-1,0,2)求围成平行四边形面积2,平行于此平行四 2020-06-11 …
我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差 2020-06-14 …
最好不用方程.把一些棱长2厘米的立方体摆成下面的形状.摆放层数 1 2 3 4 5 6 7 8 9 2020-06-27 …