设函数f（x）=lnx+ax，a∈R．（Ⅰ）当a=e（e为自然对数的底数）时，求f（x）的极小值；（Ⅱ）讨论函数g（x）=f′（x）-x3零点的个数；（Ⅲ）若对任意m>n>0，f(m)-f(n)m-n<1恒成立，求a的取

Question

设函数f（x）=lnx+(a)/(x)，a∈R．
（Ⅰ）当a=e（e为自然对数的底数）时，求f（x）的极小值；
（Ⅱ）讨论函数g（x）=f′（x）-(x)/(3)零点的个数；
（Ⅲ）若对任意m>n>0，(f(m)-f(n))/(m-n)<1恒成立，求a的取值范围．

Answer 1

（Ⅰ）f（x）的定义域为（0，+∞），
当a=e时，f（x）=lnx+(e)/(x)，则f′（x）=(x-e)/(x2)，
∴当x∈（0，e）时，f′（x）<0，f（x）在（0，e）上单调递减；
当x∈（e，+∞）时，f′（x）>0，f（x）在（e，+∞）上单调递增，
∴x=e时，f（x）取得极小值f（e）=lne+(e)/(e)=2，
∴f（x）的极小值为2；
（Ⅱ）由题设g（x）=f′（x）-(x)/(3)=(1)/(x)-(a)/(x2)-(x)/(3)（x>0），
令g（x）=0，得a=-(1)/(3)x³+x（x>0），
设φ（x）=-(1)/(3)x³+x（x≥0），则φ′（x）=-x²+1=-（x-1）（x+1），
当x∈（0，1）时，φ′（x）>0，φ（x）在（0，1）上单调递增；
当x∈（1，+∞）时，φ′（x）<0，φ（x）在（1，+∞）上单调递减，
∴x=1是φ（x）的唯一极值点，且是极大值点，
∴x=1也是φ（x）的最大值点，
∴φ（x）的最大值为φ（1）=(2)/(3)．
又φ（0）=0，结合y=φ（x）的图象（如图所示），可知

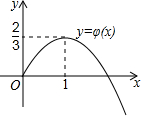
①当a>(2)/(3)时，函数g（x）无零点；
②当a=(2)/(3)时，函数g（x）有且只有一个零点；
③当0<a<(2)/(3)时，函数g（x）有两个零点；
④当a≤0时，函数g（x）有且只有一个零点（x>0），
综上所述，当a>(2)/(3)时，函数g（x）无零点；
当a=(2)/(3)或a≤0时，函数g（x）有且只有一个零点；
当0<a<(2)/(3)时，函数g（x）有两个零点；
（Ⅲ）对任意的m>n>0，(f(m)-f(n))/(m-n)<1恒成立，
等价于f（m）-m<f（n）-n恒成立（*），
设h（x）=f（x）-x=lnx+(a)/(x)-x（x>0），
∴（*）等价于h（x）在（0，+∞）上单调递减，
由h′（x）=(1)/(x)-(a)/(x2)-1≤0在（0，+∞）上恒成立，
得a≥-x²+x=-（x-(1)/(2)）²+(1)/(4)（x>0）恒成立，
∴a≥(1)/(4)（对a=(1)/(4)，h′（x）=0仅在x=

作业帮用户 2017-02-14

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议